Cours de maths à partir de 9.90 €/heure
Cours maths 5ème
Symétrie centrale - introduction
La notion de symétrie par rapport à un point sera introduite avant d'aborder la construction du symétrique d’un point, d’un segment, d’une figure plus complexe (angle, cercle) par rapport à un point; Il sera ensuite montré comment reconnaître deux figures symétriques par rapport à un point.
Activité : images symétriques
 Observons la situation suivante :
Observons la situation suivante :
Que se passe-t-il si on fait tourner l’image 1 d’un demi tour autour du point O ?
 Si on fait tourner l'image 1 d'un demi-tour autour du point O,elle vient se superposer à l'image 2.
Si on fait tourner l'image 1 d'un demi-tour autour du point O,elle vient se superposer à l'image 2.
Activité : bilan et définitions
 Les images 1 et 2 sont symétriques par rapport au point O.
Les images 1 et 2 sont symétriques par rapport au point O.
Le point O est appelé le « centre de la symétrie » et cette symétrie est une « symétrie centrale ».
Observation : symétrique d’un point
 Observons la figure ci-contre:
Observons la figure ci-contre:
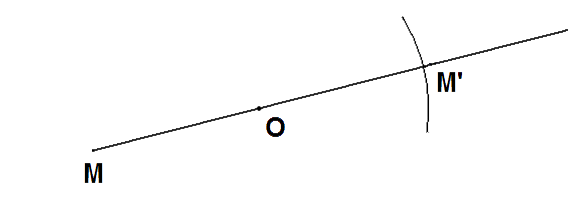
Les points M, O et M’ sont alignés dans cet ordre.
Les segments [MO] et [OM'] ont la même longueur.
Le point O est donc le milieu du segment [MM'].
Le point M' est le symétrique du point M par rapport au point O.
 Le symétrique d'un point M dans la symétrie de centre O est le point M' tel que O soit le milieu du segment [MM'].
Le symétrique d'un point M dans la symétrie de centre O est le point M' tel que O soit le milieu du segment [MM'].
Construction d'une symétrie centrale
 Pour construire le symétrique d'un point M par rapport à un point O, il faut :
Pour construire le symétrique d'un point M par rapport à un point O, il faut :
Tracer la demi-droite [MO).
Tracer le cercle de centre O passant par M.
Le cercle coupe la demi-droite ; le point d'intersection est le point M' cherché
En fait, la plus part du temps, on tracera seulement un arc de cercle de centre O et de rayon OM coupant la demi droite [MO) en M'.
Reconnaître deux points symétriques
Voici 3 figures
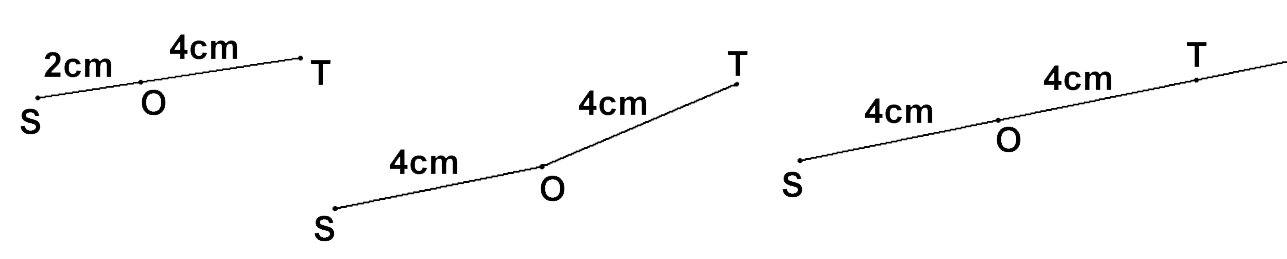
Dans quel(s) cas les points S et T sont-ils symétriques par rapport au point O?
Dans la dernière figure, le point O est le milieu du segment [ST]. C'est la seule figure qui corresponde à une symétrie par rapport à O : les points S, O et T sont alignés dans cet ordre et SO = OT.
Propriété : milieu et symétrie
Si un segment a pour milieu le point O, alors les extrémités de ce segment sont symétriques par rapport à O.
Activité : symétrique d’un segment
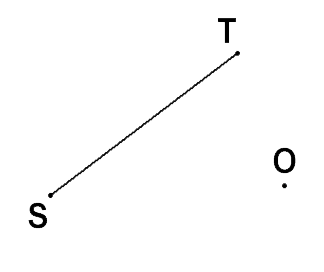 On donne deux points S et T quelconques du plan. Quel est le symétrique du segment par rapport à un point O ?
On donne deux points S et T quelconques du plan. Quel est le symétrique du segment par rapport à un point O ?
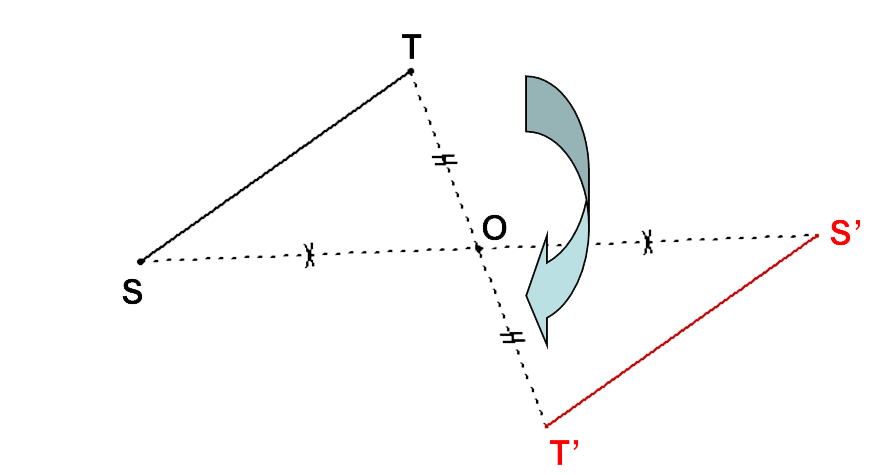 Reportons la figure sur un calque et faisons la tourner autour du point O.
Reportons la figure sur un calque et faisons la tourner autour du point O.
On obtient alors les points S’, T’ et le segment [S’T’].
Le segment [ST] et le segment [S'T'] sont symétriques par rapport au point O.
On remarque qu’ils sont superposables.
Propriété : symétrique d’un segment
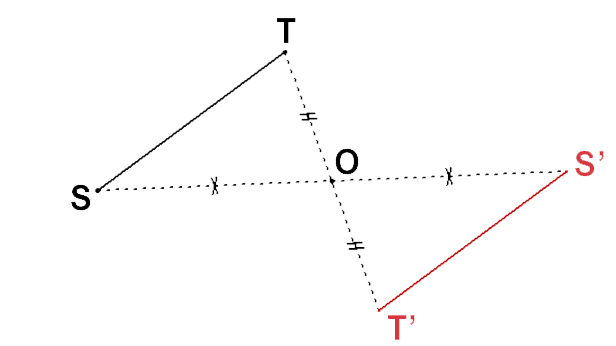 Si deux segments sont symétriques par rapport à un point O, alors les deux segments ont la même longueur.
Si deux segments sont symétriques par rapport à un point O, alors les deux segments ont la même longueur.
On dit que
« la symétrie centrale conserve les longueurs »
Propriété : figures symétriques
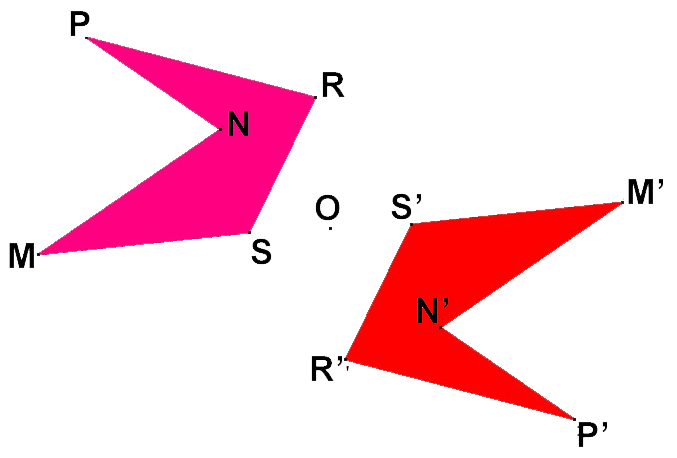 Les deux figures MNPRS et M'N'P'R'S' sont obtenues par un demi-tour autour du point O.
Les deux figures MNPRS et M'N'P'R'S' sont obtenues par un demi-tour autour du point O.
Elles sont symétriques par rapport au point O.
Elles sont superposables.
Elles ont donc le même périmètre et la même aire.
Deux figures symétriques par rapport à un point O ont le même périmètre et la même aire.
Propriétes angles symétriques
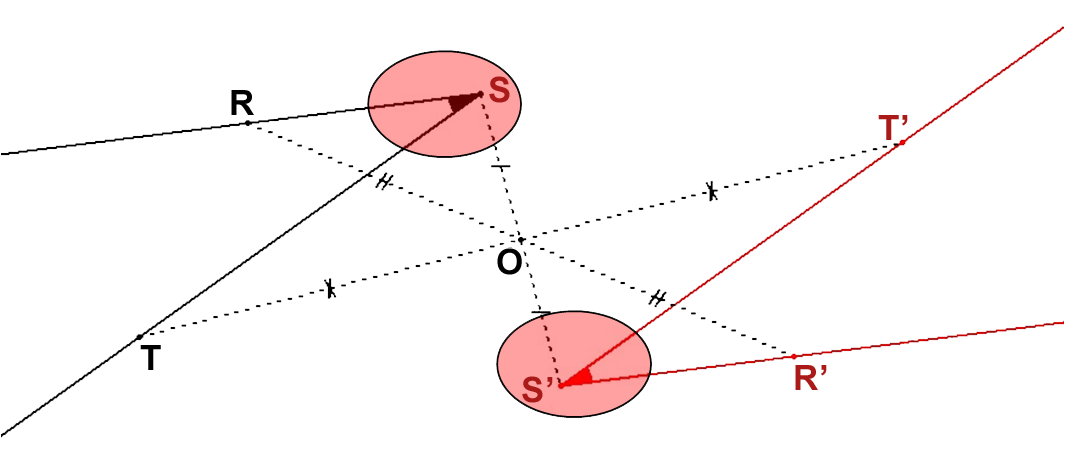
On dit parfois que
« la symétrie centrale conserve les mesures des angles ».
Deux angles symétriques par rapport à un point O ont la même mesure.
Propriété : cercles symétriques
 Les deux cercles sont symétriques par rapport au point O.
Les deux cercles sont symétriques par rapport au point O.
Les centres C et C' des deux cercles sont symétriques par rapport au point O.
Les deux cercles ont le même rayon : CR = C'R'.
Deux cercles symétriques par rapport à un point O ont des centres symétriques par rapport à O et des rayons égaux.
Cours complémentaires
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.