.gif)
.gif)
.gif)
Soustraction
Soustractions : Ce cours revient sur la soustraction des nombres décimaux en précisant le vocabulaire : définition de la différence et des termes d’une soustraction. La notion d’ordre de grandeur d’une différence qui permet de contrôler ou d’anticiper un résultat est ensuite abordée. Pour terminer, ce cours utilise la soustraction pour résoudre une équation : comment trouver le nombre à ajouter pour obtenir un résultat donné ? |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Vocabulaire
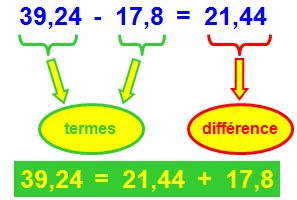
| Définition : Le résultat d’une soustraction s’appelle une différence et les nombres que l’on soustrait entre eux sont les termes de la différence. |
La différence entre deux nombres est le nombre qu’il faut ajouter à l’un pour trouver l’autre.
Exemple :
Remarque
Attention !
.jpg)
Dans le calcul d’une somme l’ordre des termes n’a pas d’importance.
Par contre, dans une soustraction on ne peut pas changer l’ordre des termes.
Poser une soustraction
Pour poser une soustraction on doit aligner verticalement les chiffres des unités des deux termes de la différence.
Exemple :
Ordre de grandeur d’une différence
Dans le calcul d’une différence, lorsque l’on remplace les termes par des nombres plus simples mais très proches, le résultat obtenu que l’on obtient facilement par calcul mental, est appelé ordre de grandeur de la différence.
Exemple :
Recherchons un ordre de grandeur de 2 789,41 – 302,56.
302,56 est proche de 300
La valeur exacte de 2 789,41 – 302,56 est : 2 789,41 – 302,56 = 2 486,85.
Remarque :
Calculer un ordre de grandeur d’une différence permet de prévoir ou de vérifier un résultat.
Application : résoudre une équation
La soustraction permet de chercher un terme inconnu d’une somme.
Exemple :
Dans un collège il y a 483 élèves.
Sur ces 483 élèves, 251 sont des garçons.
Combien y a-t-il de filles dans ce collège ?
On a :
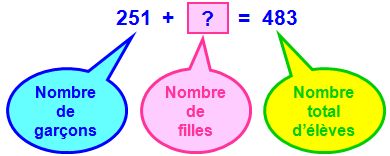
Pour trouver le nombre de filles, on doit calculer
.jpg){kind=small}
Il y a donc 232 filles dans ce collège. Rechercher un terme inconnu d’une somme s’appelle résoudre une équation du type :
Cours complémentaires : |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)