Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Fonctions affines - introduction
Ce cours a pour objectifs de faire manipuler le vocabulaire relatif aux fonctions, les calculs d’images et d’antécédents et de travailler sur la représentation graphique d’une fonction affine.
Activité : énoncé
Pour s’inscrire à la salle de sport « en forme », il faut acheter une carte d’abonnement d’un montant de 30 € correspondant aux frais d’inscriptions puis régler 1,50 € par séance.
Audrey a pris cet abonnement et s’est rendu 20 fois à la salle au cours du 1er trimestre.
Elle calcule sa dépense :
30 + 20 × 1,5 = 30 + 30 = 60 €

Activité : questions
1. a) Quatre de ses amies désirent aussi calculer le montant total de leurs dépenses.
Voici le tableau obtenu :
30 + 15 × 1,5 = 30 + 22,5 = 52,5 €
30 + 18 × 1,5 = 30 + 27 = 57 €
30 + 25 × 1,5 = 30 + 37,5 = 67,5 €
30 + 32 × 1,5 = 30 + 48 = 78 €
b) Ce tableau est-il un tableau de proportionnalité ? Justifier.
Donc ce n’est pas un tableau de proportionnalité.
On exprime la dépense total en multipliant le nombre de séance par 1,5 puis on ajoute 30. Plus généralement, si x désigne le nombre de séances, pour exprimer en fonction de x la dépense total, on applique le programme de calcul suivant :
Ce procédé qui a tout nombre x associe le nombre 1,5x + 30 définit une fonction affine
Si on appelle f la fonction, on note : f : x → 1,5 x + 30
Activité : résumé
Ce procédé qui a tout nombre x associe le nombre 1,5 x + 30 définit une fonction affine f.
On note : f : x → 1,5 x + 30
Le nombre 1,5x + 30 est appelé « l’image de x par la fonction f » ;
On note f(x) cette image, on lit « f de x » et on écrit f(x) = 1,5 x + 30.
Définitions et notations de fonctions affines
Soit a et b deux nombres fixés.
En associant à chaque nombre « x » un nombre « ax + b» appelé image de x, on définit une fonction affine f.
On notera
cette fonction f : x → ax + b
L’image de x sera notée f(x).
Remarques :
♦ Une fonction linéaire est une fonction affine particulière.
En effet, f : x → ax peut s’écrire f : x → ax + 0
♦ f : x → ax + b est une fonction affine,
g : x → ax est la fonction linéaire associée à f .
Cours : exemple
Exemple :
Soit f la fonction affine définie par f : x → 2 x + 7
Alors l’image de 5 est f(5) = 2 × 5 + 7 = 10 + 7 = 17
L’image de (-3) est f(- 3) = 2 × (- 3) + 7 = - 6 + 7 = 1
Le nombre qui a pour image 8 par f est le nombre x tel que :
2 x + 7 = 8
2 x = 8 – 7
2 x = 1
x = 1 ÷ 2 = 0,5
Le nombre qui a pour image 8 par f est 0,5.
Remarque :
On peut regrouper ces résultats dans un tableau : 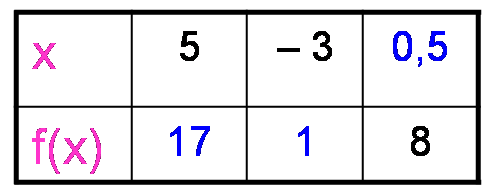
Représentation graphique de fonctions affine
La représentation graphique de la fonction f est l’ensemble de tous les points M de coordonnées ( x ; f(x) ) obtenus en prenant toutes les valeurs possibles de x.
Activité : observation
f est la fonction affine : f : x → 2 x – 3.
1) Calculer f(0) ; f(1) ; f(3) ; f(-1).
f(0) = 2 × 0 – 3 = -3
f(1) = 2 × 1 – 3 = 2 – 3 = -1
f(1) = 2 × 1 – 3 = 2 – 3 = -1
f(-1) = 2 × (-1) – 3 = -2 – 3 = - 5
2) Dans le repère ci-contre, placer les points :
A (0 ; f(0) ) ;
B (1 ; f(1) ) ;
C (3 ; f(3) ) ;
D (-1 ; f(-1) ) ;
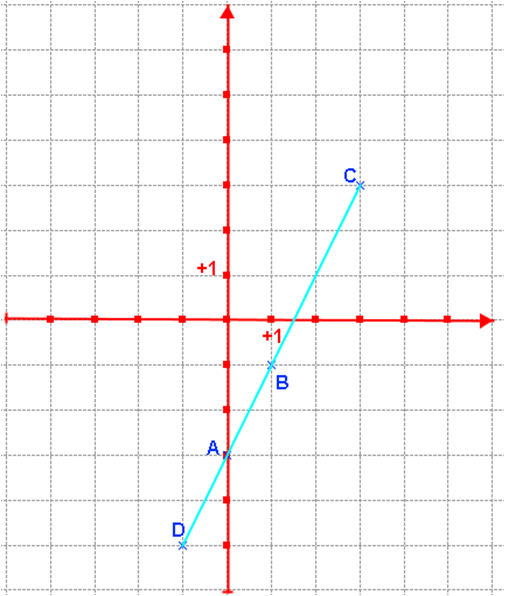
3) Qu’observe-t-on ?
Les points A, B, C et D semblent alignés.
Cours : représentation graphique de fonctions affines
Propriétés :
La représentation graphique d’une fonction affine f : x → ax + b est une droite d’équation y = ax + b.
Cette droite est parallèle à la droite représentant la fonction linéaire associée et passe par le point (0 ; b).
Remarque :
Pour la construire, il suffit de connaître deux points (abscisses x et leurs images f(x) )
Définitions :
a est le coefficient directeur de la droite d ; b est l’ordonnée à l’origine.
Cours : exemple
Exemple :
Soit g la fonction affine définie par g : x → 2x – 5.
Sa représentation graphique est une droite.
g(0) = -5 et g(1) = 2 ×1 – 5 = 2 – 5 = - 3
La fonction linéaire associée à g est : f : x → 2 x
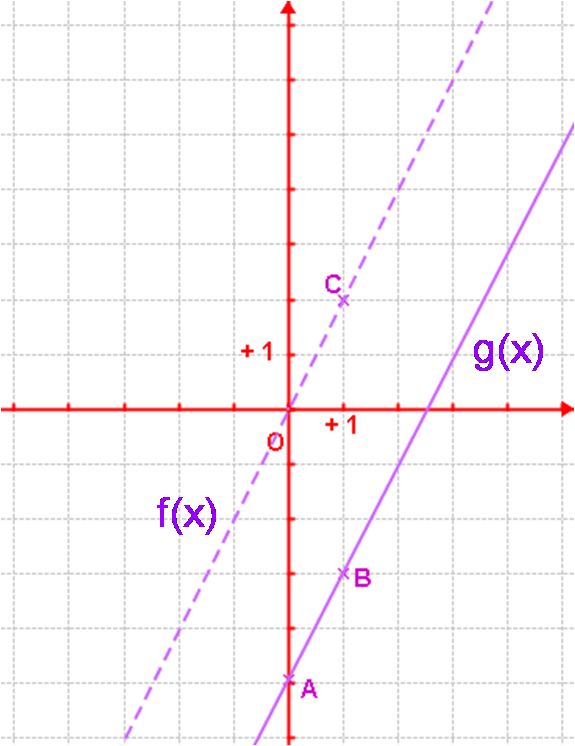
Cours complémentaires
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.