Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Notion de fonctions
Ce module a pour objectifs de faire découvrir la notion de fonctions et le vocabulaire associé.
Nous travaillerons à partir de formules, tableaux et graphiques.
Activité : A l’usine
Une usine remplit des boîtes de conserve de mais.
Pour cela, elle utilise une chaine composée de 2 machines :
- La machine R remplit la boite.
- La machine C pose le couvercle sur la boîte et le scelle

L’ordre de passage est-il important ?
Oui, l’ordre de passage est important : on ne peut pas fermer la boîte avant de l’avoir remplie.
Activité : En mathématiques
Voici un programme de calcul :
Je choisis un nombre x
J’ajoute 5 à mon nombre x
Je prend le triple du nombre obtenu
Je note y le résultat.
Exprimer y en fonction de x.
Pour résoudre ce problème, j’ai utilisé « 2 machines mathématiques » :
la 1ère « ajoute 5 » et la 2nde « multiplie par 3 ». L’ordre est-il important ?
A nouveau, l’ordre de passage est important : il détermine les priorités opératoires.
Bilan de l’activité
En mathématique, une « machine » ou une « chaine de machine » qui transforme un nombre est appelé une fonction.
Exemple :
Ainsi, la chaine ci-dessus est une fonction. On la note : f : x → 3x + 15
x est le nombre de départ, on l’appelle
l’antécédent.
3x + 15 est le nombre d’arrivée.
On le note f(x) = 3x + 15 et on l’appelle
l’image de x.
Vocabulaire des fonctions
Une fonction de la variable x est un outil mathématique qui au nombre x fait correspondre un unique nombre f(x).
Exemple :
A un nombre x, on fait correspondre son carré.
On définit ainsi une fonction, que l’on peut, par exemple, notée f : x → x2
x est le nombre de départ, on dit que c’est
un antécédent de x²
f(x) = x² est appelé
l’image de x.
Cours : exemple de fonctions
Soit f la fonction qui à x associe son double.
On la note
f: x → 2x.
Alors l’image de 5 est
f(5) = 2 × 5 = 10
L’image de (-3) est
f(- 3) = 2 × (- 3) = - 6
L’antécédent de 8 par f est
x = 8 ÷ 2 = 4
Remarque : On peut regrouper ces résultats dans un tableau.
Cours : définition d’une fonction
Il existe 3 façons de définir une fonction :
Avec une formule
Exemple : f : x → x2
Avec un tableau
Exemple :
Avec un graphique
Cours : représentation graphique d'une fonction
Soit f : x → x2.
On choisit un repère.
La représentation graphique de f est l’ensemble des points de coordonnées (x ; f(x) ) dans ce repère.
Attention :
Les valeurs lues sur un graphique ne sont pas toujours des valeurs exactes.
Il s’agit le plus souvent de valeurs approchées.
Représentation graphique : exemple
Voici la représentation graphique de la fonction f : x → x2.
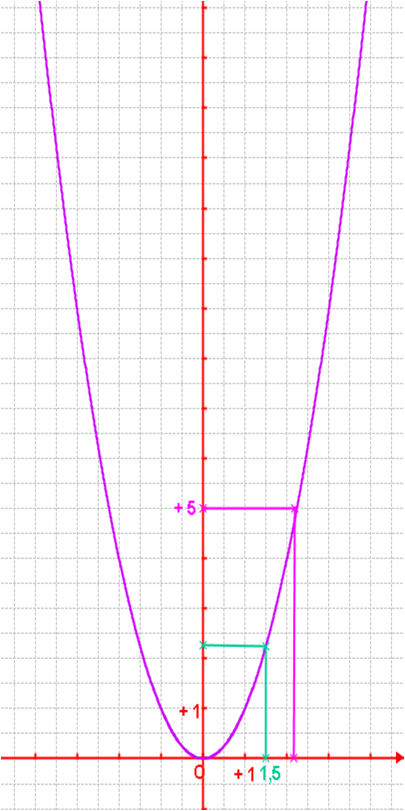
Graphiquement, on trouve que :
l’image de 1,5 est environ 2,25
Par le calcul, on trouve que :
l’image de 1,5 est : 1,5² = 2,25
Graphiquement, on trouve que :
l’antécédent de 5 est environ 2,2
Par le calcul, on trouve que :
l’antécédent de 5 est : √5 ≈ 2,24
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.