.gif)
.gif)
.gif)
Réciproque du théorème de Thalès
Cours maths 3ème
Réciproque du théorème de Thalès : Ce cours a pour objectifs de démontrer, puis d’utiliser la réciproque de la propriété de Thalès. |
| ► Sommaire cours maths 3ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Activité : Des cas particuliers
Dans chacun des cas suivants, comparer :
Montrer que les droites (MN) et (BC) sont parallèles.
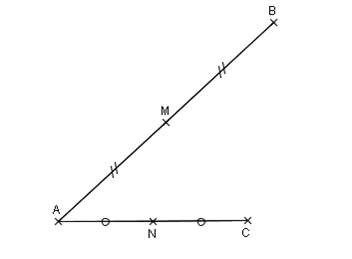
Activité : Figure 1
.png){kind=small}
Traçons les droites (MN) et (BC).
M est le milieu de [AB] donc :
N est le milieu de [AC] donc :
Ainsi :
On sait que :
ABC est un triangle, M est le milieu de [AB], N est le milieu de [AC]
Or :
dans un triangle, si une droite joint les milieux de deux côtés alors elle est parallèle au troisième côté
Donc :
(MN) // (BC)
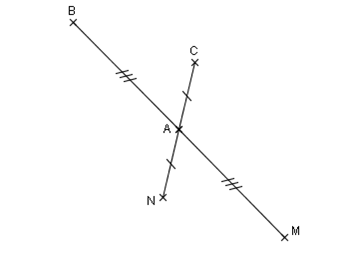
Activité : Figure 2
.png)
Traçons les droites (MN) et (BC).
AM = AB donc
.png)
AN = AC donc
.png)
Ainsi :
.png)
On sait que :
M et B sont symétriques par rapport à A
N et C sont symétriques par rapport à A
D’où :
(MN) et (BC) sont symétriques par rapport à A
Or :
si deux droites sont symétriques par rapport à un point, alors elles sont parallèles
Donc :
(MN) // (BC)
Dans chacun des cas suivants,
Placer M et N sur chaque figure puis répondre à la question :
« Les droites (MN) et (BC) semblent-elles parallèles ? »
.png)
M є [Ax’), N є [Ay’), k = 2÷5 ... (MN) et (BC) semblent-elles parallèles ? Oui
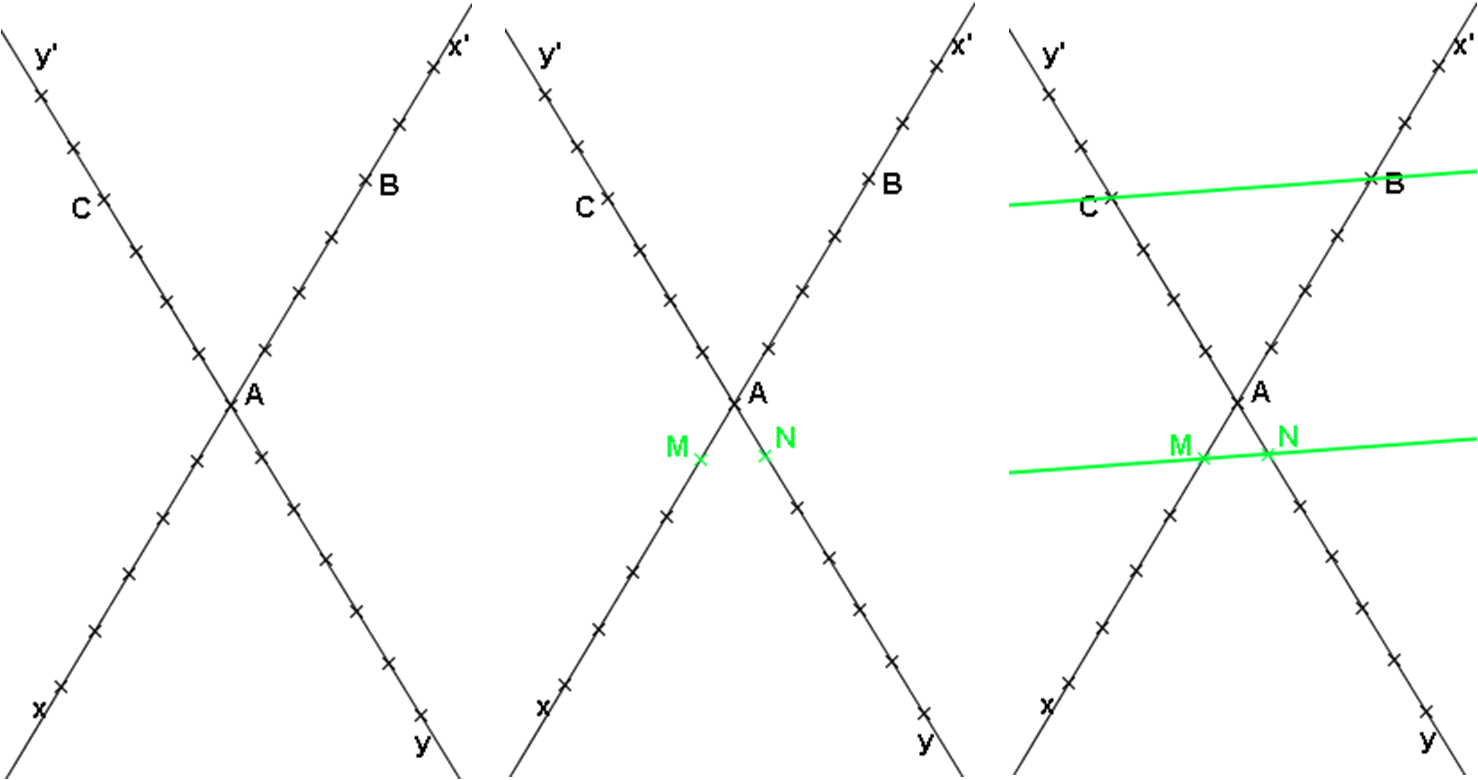
M є [Ax), N є [Ay), k = 1÷4 ... (MN) et (BC) semblent-elles parallèles ? Oui
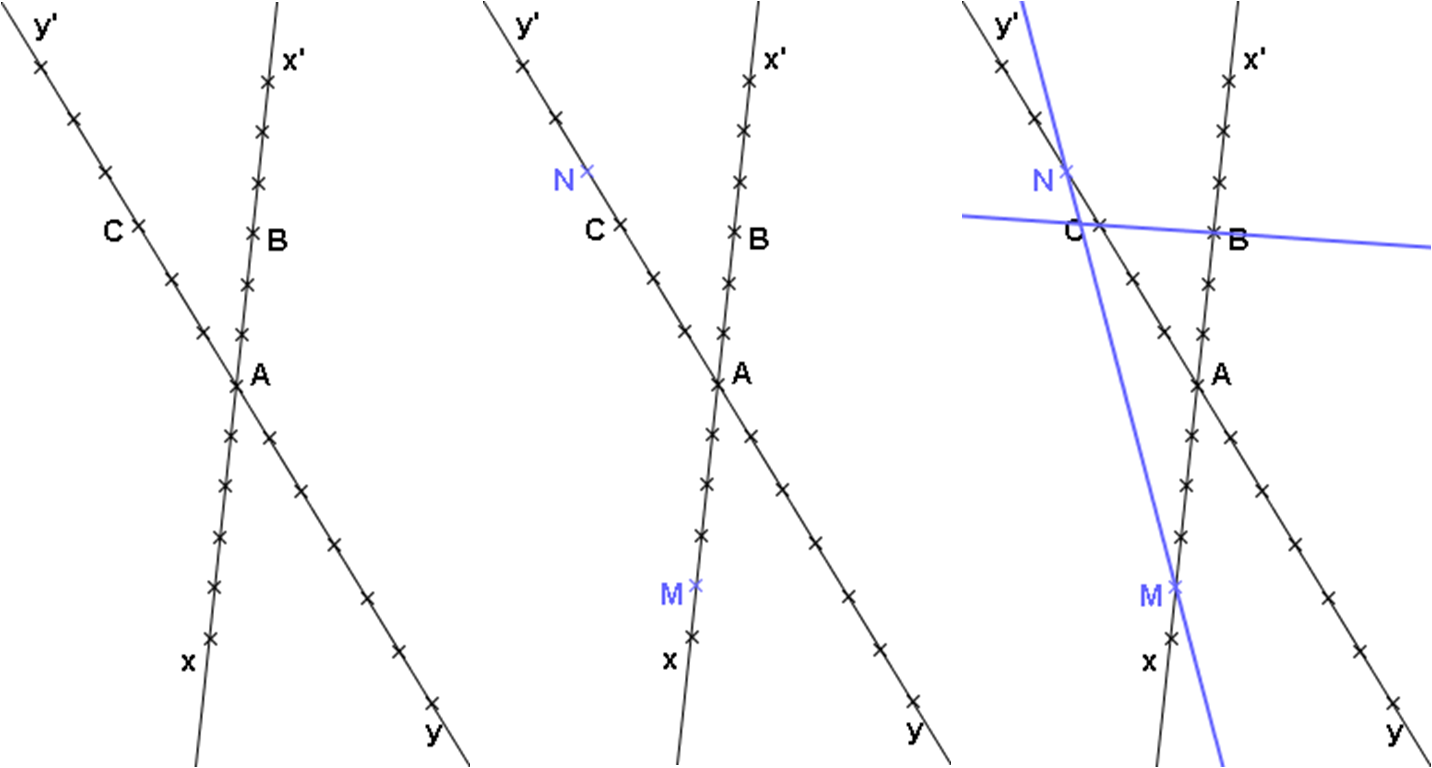
M є [Ax), N є [Ay’), k = 4÷3 ... (MN) et (BC) semblent-elles parallèles ? Non
Quelle condition faut-il ajouter à celle de l’égalité des rapports pour que les droites (MN) et (BC) soient parallèles ?Il faut en plus que les points A, B, M et les points A, C, N soient alignés et dans le même ordre.
Réciproque du théorème de Thalès
Enoncé de la réciproque du théorème de Thalès :
Soient (d) et (d’) deux droites sécantes en A.
Soient B et M deux points de (d) distincts de A.
Soient C et N deux points de (d’) distincts de A.
Si les points A, B, M et les points A, C, N sont alignés dans le même ordre et
Alors les droites (MN) et (BC) sont parallèles.
A quoi sert ce théorème ?
Ce théorème sert à montrer que deux droites sont parallèles.
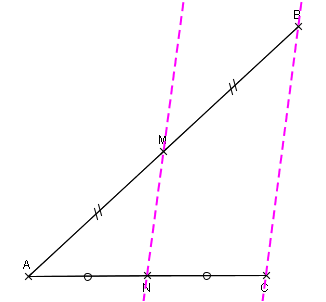
Exemple d’application de la réciproque du théorème de Thalès
Exemple :
AC = 10 cm
AE = 4 cm
AD = 6 cm
AB = 15 cm
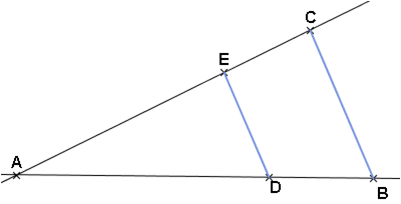
Montrer que les droites (ED) et (BC) sont parallèles.
On sait que :
les points A, E, C et les points A, D, B sont alignés dans le même ordre etD’après la réciproque du théorème de Thalès :
les droites (ED) et (BC) sont parallèles
Cours complémentaires : |
| ► Sommaire cours maths 3ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)