.gif)
.gif)
.gif)
Opérations sur les fonctions
Cours maths 1ère S
Opérations sur les fonctions : Opérations sur les fonctions |
| ► Sommaire cours maths 1ère S A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Rappel
Définition :
Soit D une partie de R.
Définir une fonction f de D dans R c’est associer à tout nombre réel x de D un nombre réel unique noté f(x).
On note alors :
Pour tout x
.png){kind=small}
D, le nombre réel f(x) s’appelle l’image de x par f.Si y
R, tout nombre réel xD tel que f(x) = y est un antécédent de y par f.L’ensemble des nombres réels possédant une image par f s’appelle l’ensemble de définition de la fonction f.
On le note Df.
Egalité de deux fonctions
Définition :
Soient f et g deux fonctions.
On dit que les deux fonctions f et g sont égales si :
(1) f et g ont le même ensemble de définition D.
(2) Pour tout x de D, f(x) = g(x).
On note alors f = g.
Exemples :
Considérons les deux fonctions f et g définies par :
Les deux fonctions f et g sont définies sur R et on a, pour tout x
R, f(x) = g(x)
Les deux fonctions f et g sont donc égales :
f = g
Comparaison de fonctions
Définition
Soient f et g deux fonctions et I un intervale inclus dans Df et dans Dg
On dit que f est inférieure ou égale à g sur l si, pour tout x
l on a : f(x) < g
On note alors f < g
Interprétation graphique
Soient f et g deux fonctions, I un intervalle inclus dans Df et dans Dg et Cf et Cg les courbes représentatives des fonctions f et g revient à étudier les positions relatives des leurs courbes représentatives des fonctions f et g dans un repère.
Pour cela on étudie le signe de f(x) - g(x), pour x
I
La fonction f est inférieure ou égale à la fonction g sur I, si sa courbe représentative est au dessous de celle de g.
Exemple :
Soient f et g les deux fonctions définies sur R par :.png)
f(x)=(x+2)(x-1)(x-3)
et
g(x)=(x+2)(3-x)
On a
f(x)-g(x) = (x+2)(x-1)(x-3)-(x+2)(3-x)
= (x+2)(x-3)(x-1+1)
= x(x+2)(x-3)
Opérations algébriques sur les fonctions
.png)
Composition des fonctions
.png)
.png)
Attention !
En général les deux fonctions g º f et f º g sont différentes.
Fonctions associées
Soient f et g deux fonctions et soient Cf et Cg les courbes représentatives de f et de g respectivement dans un repère orthogonal
.png){kind=small}
Nous allons voir comment obtenir la courbe représentative de g à partir de celle de f dans quelques cas simples.
.png){kind=small}
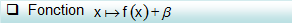
Soit g la fonction définie par
.png){kind=small}
La courbe représentative Cg de g s’obtient à partir de celle de f par une translation de vecteur
.png){kind=small}
Propriété :
Les fonctions f et g ont le même sens de variation.
.png){kind=small}
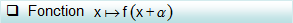
Soit g la fonction définie par
.png){kind=small}
La courbe représentative Cg de g s’obtient à partir de celle de f par une translation de vecteur
.png){kind=small}
Le sens de variation de g sur un intervalle [a,b] est identique à celui de f sur l’intervalle translaté [ a -
, b - ].png){kind=small}
Soit g la fonction définie par
.png){kind=small}
La courbe représentative Cg de g s’obtient à partir de celle de f par une translation de vecteur
.png){kind=small}
.png){kind=small}
Soit g la fonction définie par-
.png){kind=small}
La courbe représentative Cg de g s’obtient point par point à partir de la courbe de f, en multipliant pour chaque x, l’ordonnée f(x) par λ.
.png)
Propriété :
- Si λ > 0, λ f et f ont le même sens de variation sur un intervalle.
- Si λ < 0, λ f et f ont des sens de variation contraires sur un intervalle.
Propriété :
La somme de deux fonctions croissantes sur un intervalle est une fonction croissante sur cet intervalle.
La somme de deux fonctions strictement croissantes sur un intervalle est une fonction strictement croissante sur cet intervalle.
La somme de deux fonctions décroissantes sur un intervalle est une fonction décroissante sur cet intervalle.
La somme de deux fonctions strictement décroissantes sur un intervalle est une fonction strictement décroissante sur cet intervalle.
Attention !
Si f et g n’ont pas le même sens de variation, on ne peut donner aucun résultat général sur le sens de variation de f + g.
Sens de variation du produit de deux fonctions positives
Exemple
Propriété :
Soient f et g deux fonctions définies et positives sur un intervalle I.
Si f et g sont croissantes sur I, alors fg est croissante sur I.
Si f et g sont strictement croissantes sur I, alors fg est strictement croissante sur I.
Si f et g sont décroissantes sur I, alors fg est décroissante sur I.
Si f et g sont strictement décroissantes sur I, alors fg est strictement décroissante sur I.
Propriété :
Soient f et g deux fonctions telles que f soit monotone sur un intervalle I et g soit monotone sur un intervalle J.
On suppose que pour tout x
l, f (x)J.Alors
(1) Si f et g ont le même sens de variation sur I et J respectivement, alors g ° f est croissante sur I.
(2) Si f et g ont des sens de variation contraires sur I et J respectivement, alors g ° f est décroissante sur I.
Exemple :
Cours complémentaires : |
| ► Sommaire cours maths 1ère S A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)