Cours maths Terminale S

Similitudes

Ce module débute par une mise au point sur la notion de transformation du plan. Les différentes applications du plan croisées au cours de la scolarité sont passées en revue afin de déterminer si elles satisfont ou non à la définition de transformation.

 

1/ Transformation du plan : définition

Soit f application définie dans le plan par :

Si f possède les deux propriétés suivantes :
1° Tout point du plan a une image.
2° Tout point du plan a un antécédent unique.

Alors f est une bijection du plan dans lui-même et est appelée transformation du plan.

Propriétés

1 ° f admet alors une application réciproque, notée f-1 , qui est elle aussi une transformation du plan.
2° Si A ≠ B alors f (A) ≠ f (B). Deux points distincts ont des images distinctes.

 

1/ Transformation du plan : catalogue

les symétries axiales sont également appelées : symétries orthogonales.

Remarques:

•&nbsp La projection orthogonale n’est pas une transformation du plan car deux points distincts peuvent avoir la même image.
•&nbsp Les symétries centrales sont des cas particuliers d’homothéties et de rotations.
•&nbsp On appelle identité, notée Id, la transformation du plan par laquelle tout point du plan a pour image lui-même.
•&nbsp La translation de vecteur nul, toute homothétie de rapport 0 et toute rotation d’angle nul, sont l’identité.

 

2/ Similitudes : définition

On appelle similitude ( plane ) toute transformation du plan qui conserve les rapports de distances.

Soit f une transformation du plan :
Quels que soient A, B, C et D points du plan
ayant pour image respectives A', B', C' et D' :
f est une similitude ⇔

 

2/ Similitudes : équivalence

Théorème :

Une transformation du plan est une similitude
si et seulement si
elle multiplie les distances par un réel k.

Ce réel k est appelé le rapport de la similitude.

Remarque :

Les distances étant des réels positifs, on a donc : k > 0.
Grâce à ce théorème, nous pouvons en déduire que toutes les transformations rencontrées dans notre scolarité sont des similitudes.

En effet, translations, rotations, réflexions conservent les distances.
Autrement dit, elles les multiplient par k = 1.
Ce sont donc des similitudes de rapport 1, également appelées isométries.
Toute homothétie de rapport k, multiplie les distances par, attention : lkl
Il s’agit donc d’une similitude> de rapport lkl

 

2/ Similitudes : composition

Théorèmes :

La composée d’une similitude de rapport k et d’une similitude de rapport k' est une similitude de rapport : k x k'

La réciproque d’une similitude de rapport k est une similitude de rapport .

Par conséquent :
La réciproque d’une isométrie est une isométrie.

 

3/ Triangles semblables : définition.

Définition :

Deux triangles sont dits semblabes lorsque les angles de l’un sont égaux aux angles de l’autre.

Exemples :

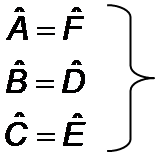Les angles homologues sont égaux donc ABC et FDE sont semblables, dans cet ordre.

On dit également que ABC et FDE sont « de même forme ».

Leurs angles homologues étant également égaux, FDE et HGP sont semblables dans cet ordre.

Remarque :

•&nbsp La somme des angles d’un triangle faisant 180°, il suffit de montrer que deux angles homologues sont égaux pour montrer que deux triangles sont semblables.

 

3/ Triangles semblables : équivalence

Théorème : ( Admis )

Deux triangles sont semblables
si et seulement si
les longueurs des côtés de l’un sont proportionnelles aux longueurs des côtés de l’autre.

Autrement dit:

Les triangles ABC et A’B’C’ sont semblables dans cet ordre
si et seulement si

 

3/ Triangles semblables et similitudes

Propriété :

Les similitudes conservent l’alignement.
Autrement dit :
Si A, B et C ont pour images respectives A’, B’ et C’ alors : A, B, C alignés ⇒ A’, B’, C’ alignés

Démonstration :

* Soient A, B et C trois points alignés dans cet ordre, alors AC = AB + BC.
* Soit s une similitude de rapport k.
s multiplie les distances par k donc : A’C’ = kAC = kAB +kAC = A’B’+B’C’.
- Les points A’, B’ et C’ sont donc alignés dans cet ordre.

Conséquence :

L’image d’un triangle par une similitude est un triangle.

Démonstration :

* Soit le triangle ABC et soient A’, B’ et C’ images respectives de A, B et C par une similitude s.
Supposons que A’B’C’ ne soit pas un triangle alors A’, B’ et C’ sont alignés.

- Donc, A, B et C images de A’, B’ et C’ par la réciproque de s sont alignés.
- Car la réciproque de s est une similitude et conserve, de ce fait, l’alignement.
- Or, ABC est un triangle donc A’, B’ et C’ ne peuvent être alignés, A’B’C’ est un triangle.

Théorème :

L’image d’un triangle par une similitude est un triangle qui lui est semblable.

Démonstration :

D’après la conséquence, l’image d’un triangle ABC par une similitude de rapport k est un triangle.
Et la similitude multipliant les distances par k, les côtés de A’B’C’ valent k fois ceux de ABC.
ABC et A’B’C’ ont des côtés de longueurs proportionnelles, ils sont donc semblables.

Réciproque : ( admise )

Si le triangle A’B’C’ est semblable dans cet ordre au triangle ABC
alors il existe une similitude et une seule transformant ABC en A’B’C’.
le rapport de la similitude est alors :

On a donc au final que :

Deux triangles sont semblables
si et seulement si
il existe une similitude transformant l’un en l’autre.

On comprend maintenant mieux le choix du terme « similitude » pour qualifier ce type de transformations.

 

4/ Triangles isométriques : définition

Définition :

Deux triangles sont dits isométriques
lorsque les longueurs des côtés de l’un sont égales aux longueurs des côtés de l’autre.

Exemple :

Les côtés [AB] ; [AC] et [BC] ont même mesure que leurs côtés homologues [A’B’] ; [A’C’] et [B’C’]
donc les triangles ABC et A’B’C’ sont dans cet ordre, isométriques, ou encore « superposables ».

Propriété :

* Deux triangles isométriques ont leurs angles homologues égaux.
* Deux triangles isométriques sont donc semblables.

 

4/ Triangles isométriques et isométries

Deux triangles isométriques étant semblables,
il existe une et une seule similitude transformant l’un en l’autre.
Les mesures des côtés homologues étant les mêmes, la similitude a pour rapport 1.

La seule similitude transformant un triangle en l’autre est donc une isométrie.

D’où :

Théorème :

Si le triangle A’B’C’ est isométrique dans cet ordre au triangle ABC
alors il existe une isométrie et une seule transformant ABC en A’B’C’.

Réciproquement, l’image d’un triangle par une similitude s de rapport k est un triangle semblable, dont les côtés mesurent k fois ceux du triangle de départ.

Si s est une isométrie, k = 1 et le triangle image est alors isométrique au triangle de départ.

D’où :

Réciproque :

L’image d’un triangle par une isométrie est un triangle qui lui est isométrique.
On a donc au final que:

Deux triangles sont isométriques
si et seulement si
il existe une isométrie transformant l’un en l’autre.

 

4/ Triangles isométriques : démonstrations

Les trois techniques employées pour montrer que deux triangles sont isométriques sont les suivantes :

Technique n° 1 :

Montrer que les côtés homologues sont 2 à 2 de même longueur.

Technique n° 2 :

Montrer que 2 côtés de l’un ont même longueur que 2 côtés de l’autre et que les angles géométriques formés par ces deux côtés sont égaux.

Technique n° 3 :

Montrer qu’un côté de l’un a même longueur qu’un côté de l’autre et que les 2 angles géométriques adjacents à chacun de ces côtés sont égaux.

Autrement dit, à une isométrie près, un triangle est entièrement défini par :
les mesures de ses trois côtés
ou
les mesures de deux de ses côtés et de l’angle géométrique qu’ils forment
ou
la mesure d’un de ses côtés et les mesures des deux angles adjacents à ce côté.

 

5/ Similitudes directes et indirectes : définition

L’image d’un triangle par une similitude est un triangle semblable, par conséquent :

Propriété :

Les similitudes conservent les angles géométriques.

Mais, qu'en est-il des angles orientés?
•&nbsp On appelle similitude directe toute similitude qui conserve les angles orientés.
Une isométrie directe est appelée un déplacement.
L’identité, les translations et les rotations sont des déplacements.
Les homothéties sont des similitudes directes.

•&nbsp On appelle similitude indirecte toute similitude qui transforme un angle en son opposé.
Une isométrie indirecte est appelée un anti-déplacement.
Les réflexions sont des anti-déplacements.

 

5/ Similitudes directes et indirectes : composition

Théorème :

•&nbsp La composée de deux similitudes directes ou de deux similitudes indirectes est une similitude directe.
•&nbsp La composée d’une similitude directe et d’une similitude indirecte est une similitude indirecte.
•&nbsp La réciproque d’une similitude directe est une similitude directe.
•&nbsp La réciproque d’une similitude indirecte est une similitude indirecte.

 

5/ Similitudes directes et indirectes : triangles

5/ Similitudes directes et indirectes : triangles

Point de vocabulaire : orientation des figures.

Un triangle ABC est qualifié de direct si l’angle orienté est positif.
Plus généralement, une figure géométrique, ABCDE par exemple, est qualifiée de directe, si la courbe passant par A, B, C, D puis E tourne dans le sens trigonométrique.

Dans le cas contraire, la figure est qualifiée d’indirecte.. On peut alors affiner les théorèmes vus plus tôt :
•&nbsp L’image d’un triangle par une similitude directe est un triangle directement semblable.
* Si le triangle de départ est, par exemple, direct, le triangle image sera également direct.

•&nbsp L’image d’un triangle par une similitude indirecte est un triangle indirectement semblable.
* Si le triangle de départ est, par exemple, indirect, le triangle image sera, lui, direct.
* Si le triangle A’B’C’ est semblable dans cet ordre au triangle ABC alors il existe une similitude et une seule transformant ABC en A’B’C’.
* Si les triangles sont de même sens, cette similitude est directe, sinon elle est indirecte.

 

6/ Similitudes : points invariants

Rappel :

On appelle point fixe ou point invariant par une transformation, tout point qui a pour image lui-même.

Théorème :

Soit s une similitude.
s possède trois points invariants non alignés si et seulement si s est l’identité.
On dira également que toute similitude « fixant » trois points non alignés est l’identité.

Théorème :

Si deux points distincts A et B sont invariants par une similitude s, alors : soit s est l’identité, soit s est la réflexion d’axe (AB).

Remarque :

Les démonstrations de ces deux théorèmes feront l’objet d’un R.O.C dans la partie exercice de votre espace membre.

 

7/ Similitudes : bilan des propriétés

Soit s similitude de rapport k :
•&nbsp s conserve l’alignement, donc :
- l’image d’une droite est une droite.
- l’image du segment [AB] est le segment [s(A)s(B)] de longueur kAB.
- s conserve les intersections.

•&nbsp s conserve, de plus, par définition, les rapports de distances donc :
- s conserve le milieu et plus généralement le barycentre.

•&nbsp s conserve les angles géométriques , donc :
- s conserve l’orthogonalité et le parallélisme.

•&nbsp L’image du cercle de centre O et de rayon r est le cercle de centre s(O) et de rayon kr.

 

8/ Avis au lecteur

Pour être capable de résoudre les exercices concernant ce module
(dans votre espace membre),
il est conseillé de réviser le module obligatoire
traitant des transformations dans le plan complexe.

Il faut en particulier connaître les écritures complexes
des translations, rotations et homothéties
ainsi que leurs propriétés géométriques.