Cours maths Terminale S

Représentations de droites

Ce module commence par les différentes façons de définir une droite de l’espace, ensuite la position relative d’une droite par rapport à un plan ; Puis, deux points clés du module : savoir passer pour une droite, d’une représentation par un système à une représentation paramétrique, ainsi que savoir montrer qu’une droite donnée est l’intersection de deux plans. Le cours se termine par l’étude exhaustive de l’intersection de 3 plans.

 

1/ Définition(s) d’une droite de l’espace

Il existe plusieurs façons de définir une droite de l’espace.

Définition N°1 d'une droite

Soit un point A de l’espace et un vecteur

Il existe une unique droite (D) passant par le point A et de vecteur directeur .

Un point M de l’espace appartient à (D)
si et seulement si :
il existe un réel k tel que :

Si M et ont pour coordonnées respectives ( x ; y ; z ) et ( a ; b ; c ) alors :
M ∈ (D) ⇔ il existe un réel k tel que :


Ce système est appelé représentation paramétrique de la droite (D).

Remarques

Prenons l’exemple de la droite (D) de représentation :

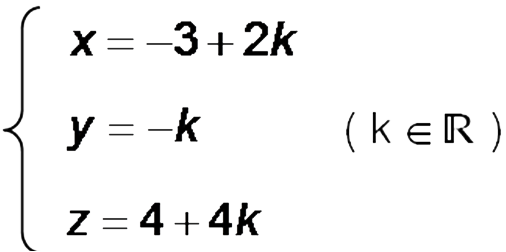
1) Le réel k est appelé le paramètre.
A chaque point de (D) correspond une et une seule valeur de k et inversement.
D’un point de vue pratique, B ( 3 ; 2 ; 5 ) appartient à (D) si et seulement si il existe k tel que :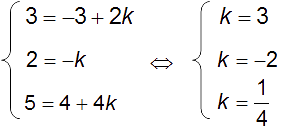



Ce qui est impossible donc B n’appartient pas à (D).
2) Le paramètre est souvent également noté à l’aide de la variable t.
3) Une droite admet une infinité de représentations paramétriques.
Il suffit en effet de changer de point d’attache ou de vecteur directeur pour obtenir un système de représentation différent.

Prenons l’exemple de la droite (D) de représentation :


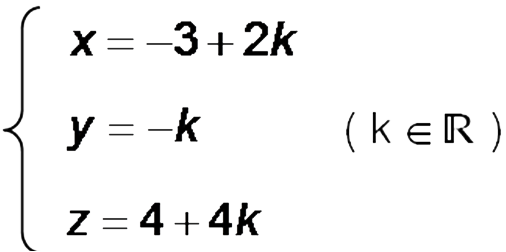
4)

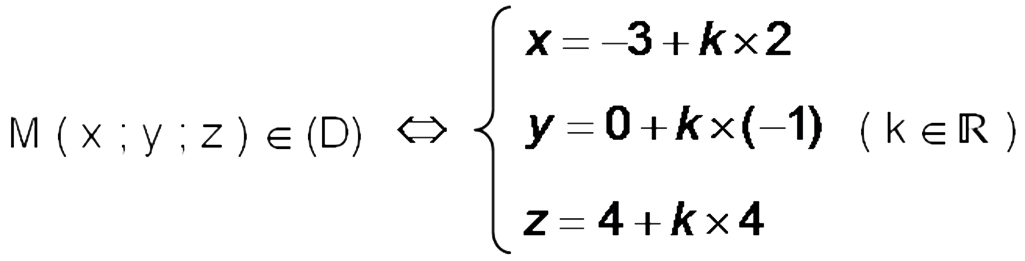
On admettra alors, que la droite (D) passe par le point 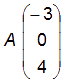et a pour vecteur directeur

 

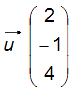
Définition N°2 d'une droite

Toute droite peut être définie comme l’intersection de deux plans sécants.


Soit par exemple les plans (P) et (Q) d’équations cartésiennes respectives :



Un point M ( x ; y ; z ) appartient alors à (D) si et seulement si ses coordonnées vérifient les équations cartésiennes de chaque plan.

(D) peut alors être définie par le système d’équations cartésiennes suivant :

 

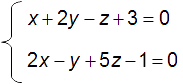
2/ Position relative d’une droite et d’un plan

Position n° 1: une droite (D) peut être parallèle à un plan.
Il existe au moins deux techniques pour le montrer.

* Soit la droite (D) passant la point A ( 1 ; 0 ; 2 ) et de vecteur directeur
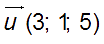
* Et soit le plan (P) d’équation cartésienne :

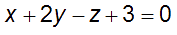
Technique n° 1 :
Montrons que est un vecteur directeur du plan (P).

Un vecteur normal à (P) est :
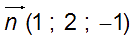
donc ces deux vecteurs sont orthogonaux.
est donc un vecteur directeur de (P).

Deux cas sont alors possibles :
- (D) peut être strictement parallèle à (P)
ou
- contenue dans (P).



Par conséquent : (D) est strictement parallèle à (P).

Technique n° 2 :
Commençons par trouver une représentation paramétrique de (D) :


Donc M(x;y;z) appartient à (D) et (P) si et seulement si il existe k tel que :

Position n° 2 : une droite (D) peut être contenue dans un plan.
Il existe au moins deux techniques pour le montrer.

* Soit la droite (D) passant la point B ( 1 ; 1 ; 6 ) et de vecteur directeur
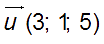
* Et soit le plan (P) d’équation cartésienne :

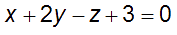
Technique n° 1 :
Nous avons montré précédemment que est un vecteur directeur de (P).

Par conséquent, la droite (D) est contenue dans le plan (P).

Technique n° 2 :
Une représentation paramétrique de (D) est :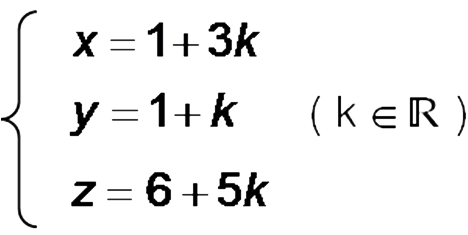

Soit M point quelconque de (D) de paramètre k.Quel que soit k.
Quel que soit k :
Donc, tout point de (D) appartient à (P).Par conséquent (D) est contenue dans (P).

Position n° 3 : une droite (D) et un plan peuvent être sécants.
Il existe au moins deux techniques pour le montrer.

* Soit la droite (D) passant la point C ( 0 ; 1 ; 4 ) et de vecteur directeur
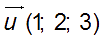
* Et soit le plan (P) d’équation cartésienne :
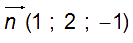
Technique n° 1 :
Montrons que n’est pas un vecteur directeur du plan (P).
Un vecteur normal à (P) est :
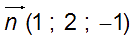
donc ces deux vecteurs ne sont pas orthogonaux.
n’est donc pas un vecteur directeur de (P).
Par conséquent, (D) qui n’est pas parallèle à (P) est sécante à (P).

Remarque

1) Si (D) est contenue dans (P), (D) n’est pas considérée comme sécante à (P).

2) Si et sont colinéaires alors (D) est orthogonale à (P).

Soit la droite (D) passant la point C ( 0 ; 1 ; 4 ) et de vecteur directeur
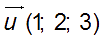
Et soit le plan (P) d’équation cartésienne :

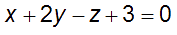
Technique n° 2 :
Une représentation paramétrique de (D) est :
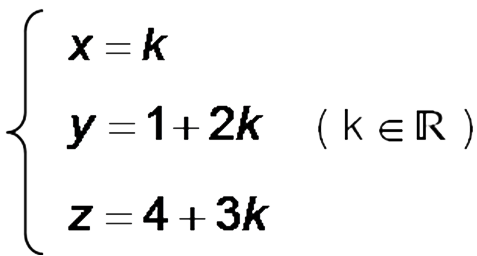
Donc M(x;y;z) appartient à (D) et (P) si et seulement si il existe k tel que :
(D) et (P) possèdent donc un unique point commun de coordonnées :


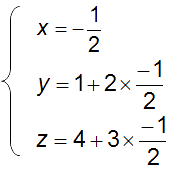
C’est le point 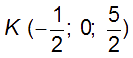(D) est donc sécante à (P).

 

3/ Position relative de deux droites

Position n° 1 : deux droites peuvent être coplanaires.
Cas n° 1 : les deux droites sont parallèles.
Pour le montrer il suffit de prouver qu’elles ont des vecteurs directeurs colinéaires.

Exemple

Soit la droite (D) passant par les points A(1;2;4) et B(-1;6;3).
Et soit le droite (D’) dont une représentation paramétrique est :


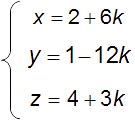
Un vecteur directeur de (D) est

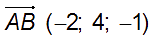
Et un vecteur directeur de (D’) est

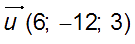
donc (D) et (D’) sont parallèles.
Il existe donc un plan les contenant toutes les deux.

Remarque

dans le cas où elles sont parallèles et confondues,il existe une infinité de plans les contenant.

Cas n° 2 : les deux droites sont sécantes.
Pour le montrer il suffit de prouver qu’elles ont un point commun, unique.

Exemple

Soient les droites (D) et (D’) de représentations paramétriques respectives :


M(x;y;z) appartient à (D) et (D’) si et seulement si il existe k et k’ réels tels que :



Cette dernière égalité sert à vérifier notre résultat :
3 - 2k = 3 - 0 = 3 et 4 + 3k’ = 4 - 1 = 3.


dont les coordonnées peuvent être calculées à l’aide de k ou k’ :

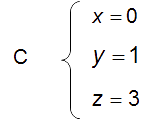
(D) et (D’) sont alors contenues dans le plan (P) passant par C et de vecteurs directeurs :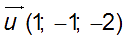
et

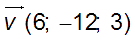
Position n° 2 : deux droites peuvent être non coplanaires.

Il n’existe alors aucun plan contenant ces deux droites.
Pour le montrer, il suffit de montrer que les deux droites ne sont ni parallèles, ni sécantes.

 

4/ Droite d’intersection de deux plans

Il est souvent demandé dans les exercices de trouver la représentation paramétrique d’une droite qui est l’intersection de deux plans.

Ou encore de montrer qu’une droite dont on connaît la représentation paramétrique est l’intersection de deux plans donnés.

Voyons les différentes stratégies qu’il est possible d’employer :

Exemple n° 1 :

Soient les plans (P) et (Q) d’équations cartésiennes respectives :


Déterminer une représentation paramétrique de la droite (D) intersection de (P) et de (Q).

(D) a pour système d’équations cartésiennes :
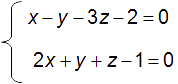
Il va donc falloir être capable de passer de ce système à une représentation paramétrique:
(D) :

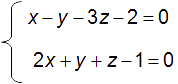
Une technique consiste à prendre une des coordonnées comme paramètre, par exemple z,puis à exprimer les deux autres coordonnées en fonction de z.

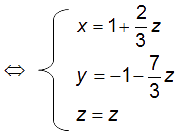
Une représentation paramétrique de (D) est donc :



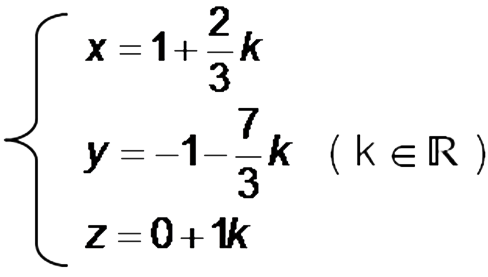
(D) passe donc par le point A ( 1 ; -1 ; 0 ) et a pour vecteur directeur

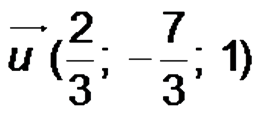
Exemple n° 2 :

Soient les plans (P) et (Q) d’équations cartésiennes respectives :


Montrer que leur intersection est la droite (D) d’équation paramétrique :

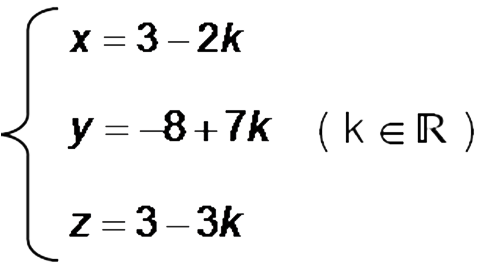
Attention !
Il faut commencer par montrer que l’intersection de ces deux plans est une droite !
Un vecteur normal à (P) est : .
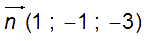
Un vecteur normal à (Q) est :

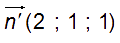
Il n’existe pas de réel k tel que 1xk=2 et (-1)xk=1 donc ces deux vecteurs ne sont pas colinéaires.
Les plans (P) et (Q) ne sont donc pas parallèles.
Ils sont par conséquent sécants, et leur intersection est une droite.

Il s’agit maintenant de montrer que (D) est contenue dans chacun des plans :

Pour tout réel k :

Tout point de (D) appartient à (P) donc (D) est contenue dans (P).

Tout point de (D) appartient à (Q) donc (D) est contenue dans (Q).
La droite (D) est donc contenue dans l’intersection de (P) et de (Q). Or, cette intersection est une droite, donc l’intersection de (P) et de (Q) est la droite (D).

Remarque

En utilisant la première méthode pour trouver l’intersection de ces deux mêmes plans, nous avions trouvé comme représentation paramétrique :

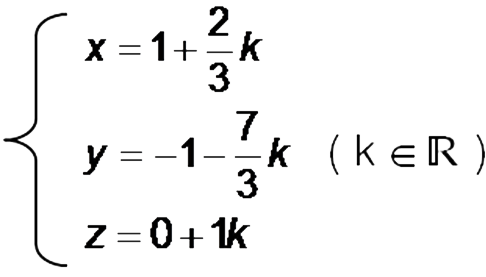
Si nous avions choisi cette méthode pour l’exemple n°2, nous aurions donc pu penser que nous nous étions trompés, alors que les deux représentations sont équivalentes.
Dans le cas où la représentation paramétrique de l’intersection est fournie par l’énoncé,il est donc conseillé d’utiliser la méthode de l’exemple n°2.

 

5/ Intersection de trois plans

Soient (P), (Q) et (R), 3 plans de l’espace.

Cas n° 1 : les plans (P) et (Q) sont parallèles.
Sous cas n° 1.1 : (P) et (R) sont parallèles.
Alors, (R) est également parallèle à (Q).


L’intersection entre (P), (Q) et (R) est alors l’ensemble vide.

Sous cas n° 1.2 : (P) et (R) sont sécants.
Alors, (R) et (Q) sont également sécants

L’intersection entre (P), (Q) et (R) est alors l’ensemble vide.
Cas n° 2 : les plans (P) et (Q) sont sécants suivant la droite (D)


Sous cas n° 2.1 : (D) est parallèle à (R).
Sous cas n° 2.1.1 : (D) est contenue dans (R).

L’intersection entre (P), (Q) et (R) est alors la droite (D).

Sous cas n° 2.1.2 : (D) est strictement parallèle à (R).

L’intersection entre (P), (Q) et (R) est alors l’ensemble vide.

Sous cas n° 2.2 : (D) et (R) sont sécants.

L'intersection entre (P) et (Q) est alors un point.

Pour trouver les coordonées de ce point, on pourra commencer par trouver une représentation paramétrique de (D) puis, chercher le point d'intersection entre (D) et (R).