Cours maths Terminale S

Produit scalaire

Ce module commence par un rappel concernant la définition de l’orthogonalité de deux vecteurs du plan. Notion pouvant être étendue à l’espace.

 

1 / Orthogonalité de deux vecteurs

Definition

- par convention, le vecteur nul est orthogonal à tout vecteur.
- soient et deux vecteurs non nuls, et A, B et C trois points tels que
Les vecteurs et sont dits orthogonaux si les droites (AB) et (AC) sont perpendiculaires.
On note : .
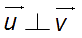Qui se lit : orthogonal à .

Remarque :

Comme il est toujours possible de trouver deux représentants coplanaires de deux vecteurs,cette définition est valable dans le plan et dans l’espace.

 

1/ Orthogonalité de deux droites

Definition

Deux droites sont dites orthogonales si les vecteurs qui les dirigent sont orthogonaux.

Mais, contrairement aux vecteurs, les droites n'ont pas de multiples représentants.

Conséquence :

Deux droites de l’espace dont orthogonales si une parallèle de l’une est perpendiculaire à une parallèle de l’autre.

Cas particulier :

Deux droites orthogonales et coplanaires sont perpendiculaires.
Deux droites orthogonales et sécantes sont donc perpendiculaires.

Sur cette figure :

Ce qui dans les deux cas, se note de la même façon :

 

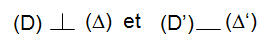
1/ Orthogonalité d’un plan et d’une droite

Définition

Une droite est orthogonale à un plan si elle est orthogonale à toute droite de ce plan.

Théorèmes :

Une droite est orthogonale à un plan si un vecteur qui la dirige est orthogonal à deux vecteurs directeurs, non colinéaires, du plan.
Ou encore, si un vecteur qui la dirige est colinéaire à un vecteur normal au plan.

Nous reviendrons en détail,dans le module suivant, sur les différentes façons d’engendrer et de définir un plan.

Conséquence :

Une droite est orthogonale à un plan si elle est orthogonale à deux droites non parallèles de ce plan.

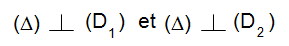
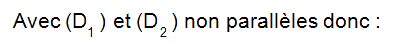
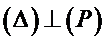
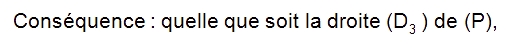
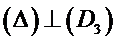
On peut démontrer l’orthogonalité entre deux droites en utilisant, par exemple, le produit scalaire,comme nous le verrons plus loin.

 

1/ Orthogonalité : plan médiateur

On appelle plan médiateur du segment [ AB ] , le plan qui est orthogonal à la droite (AB) et qui passe par le milieu de [AB].



« Le plan médiateur est à l’espace ce que la médiatrice est au plan » donc :

Propriété :

M appartient à (P) si et seulement si MA=MB.
Le plan médiateur est l’ensemble des points équidistants de A et de B dans l’espace

 

2/ Avis au lecteur

En classe de première S, le produit scalaire a été défini pour deux vecteurs du plan.
Selon les professeurs et les manuels scolaires, les définitions diffèrent
mais sont toutes équivalentes.
Dans, ce module, nous en choisirons une et les autres seront considérées comme des propriétés.

Considérons maintenant deux vecteurs et de l’espace.
Deux vecteurs étant toujours coplanaires, il existe au moins un plan les contenant.
( ou si l’on veut être plus rigoureux : contenant deux de leurs représentants )
On peut donc calculer leur produit scalaire, en utilisant la définition du produit scalaire dans ce plan.

Tous les résultats vus sur le produit scalaire dans le plan,restent donc valables dans l’espace.

Rappelons l’ensemble de ces résultats et revoyons les méthodes de calcul du produit scalaire.

 

3/ Définition du produit scalaire

Definition

Soient et deux vecteurs de l'espace. - si et sont colinéaires

- si et sont orthogonaux :

Cas particulier :

Le vecteur nul étant colinéaire et orthogonal à tout vecteur :

Conséquence :

Méthode de calcul n°1.

Une première méthode pour calculer le produit scalaire de et consiste donc à décomposer et en vecteurs soit colinéaires soit orthogonaux entre eux.

 

4/ Propriétés et méthodes de calcul

Cette première méthode s’appuie sur la définition et sur certaines propriétés algébriques du produit scalaire, à savoir :

La propriété de distributivité :

Quels que soient les vecteurs , et :

La propriété de commutativité :

Quels que soient les vecteurs et :

Propriétés qui ont pour conséquence : la propriété de double distributivité.

Exemple d’utilisation de la méthode n° 1 :

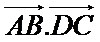colinéaires et de même sens.

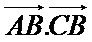orthogonaux.

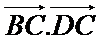orthogonaux.

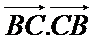Colinéaires et de sens opposés.

 

4/ Propriétés et méthodes de calcul

Autres propriétés algébriques du produt scalaire :

Quels que soient les vecteurs et







De cette dernière égalité découle la deuxième méthode de calcul du produit scalaire :

Méthode de calcul n°2 ( Méthode des normes ):

Exemple d’utilisation de la méthode n° 2 :

Et d’après le théorème de Pythagore :

Quels que soient les vecteurs et :

Où désigne le projeté orthogonal de sur .

La méthode n° 3 pour calculer un produit scalaire consistera donc à projeter l’un des vecteurs sur l’autre.

Cette méthode est en fait assez proche de la méthode n° 1, l’un des vecteurs étant décomposé en un vecteur colinéaire et un vecteur orthogonal à l’autre.

Exemple d’utilisation de la méthode n° 3 :

on peut évidemment appliquer ce resultat directement.

car les vecteurs sont colinéaires et de même sens.

Or d'après la reciproque de la droite des milieux : H est le milieu de [DC].

Remarque :

Cette méthode est simple à utiliser, si l’on choisit des représentants des vecteurs ayant la même origine.

Dans un plan orienté dans le sens direct :

Quels que soient les vecteurs et :

Deux cas sont possibles :


La méthode n° 4 consiste donc à utiliser le cosinus :

Exemple d’utilisation de la méthode n° 4 :

Or, en utilisant le triangle rectangle DBC :

Quels que soient les vecteurs et :

Outre son intérêt calculatoire, ce résultat a pour conséquence une propriété fondamentale :

Deux vecteurs et sont orthogonaux si et seulement si :

Démonstration :

La méthode de prédilection pour montrer que deux vecteurs sont orthogonaux va donc être de montrer que leur produit scalaire est nul.

Ce qui va être extrêmement simple dans un repère orthonormé :
Dans un plan muni d’un repère orthonormé :



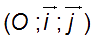
En effet :

Or les deux vecteurs de base sont orthogonaux donc leur produit scalaire est nul, d’où :



De même, dans l’espace muni d’un repère orthonormé :

Remarque :

On appelle cette forme : l’expression analytique du produit scalaire.

La méthode n° 5 consiste donc à utiliser l’expression analytique pour calculer un produit scalaire.

Conséquence :

résultat évident d’après le théorème de Pythagore

Et dans l’espace muni d’un repère orthonormé :

On peut donc grâce à ce résultat calculer la distance entre deux points de l’espace :

 

5/ Équation cartésienne d’une droite du plan

Si deux droites sont perpendiculaires à une même troisième droite alors elles sont parallèles entre elles.

Une direction de droite peut donc être définie par perpendicularité à une droite donnée,ou encore par orthogonalité à un vecteur donné.

En terme de vecteur, on ne parle alors plus de vecteur directeur mais de vecteur normal.

Une droite est entièrement définie par la donnée d’un point A et d’un vecteur normal

On a alors :

D’où, si le plan est rapporté à un repère orthonormé



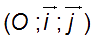
Cette équation est appelée équation cartésienne de la droite (D).

Théorème

Si 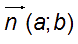est un vecteur normal à la droite (D)

alors (D) a une équation cartésienne du type : ax + by +c = 0

Exemple de recherche de l’équation cartésienne d’une droite :

Soit la droite (D) passant par A ( 1 ; 2 ) et de vecteur normal

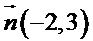
(D) a une équation cartésienne du type : −2x + 3y + c = 0

Et A ( 1 ; 2 ) ∈ (D) donc : −2 × 1 + 3 × 2 + c = 0 ⇔ − 4

D’où l’équation cartésienne de (D) : −2 + 3y −4 = 0

On peut également utiliser le produit scalaire, comme vu à la diapositive précédente :



On peut alors en déduire l’équation réduite de (D) :

Reciproque :

Si (D) a une équation cartésienne du type : ax + by + c = 0 alors le vecteur 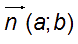est un vecteur normal de la droite (D).

Remarques pratiques : A partir d’un vecteur du plan donné, il est facile de fabriquer un vecteur qui lui est orthogonal.

Exemple :

soit .

-4 x 5 + 5 x 4=0   donc est orthogonal à .

Il suffit de croiser les coordonnées et de changer l’un des deux signes.

Connaissant un vecteur normal, on peut donc trouver un vecteur directeur

Inversement, si une droite est définie à l’aide d’un vecteur directeur,
il suffit de fabriquer à partir de ce vecteur, un vecteur qui lui est orthogonal.

Ce vecteur étant normal à la droite, on peut alors en déduire son équation cartésienne.

 

6/ Distance d’un point à une droite du plan

Soit une droite (D) et soit un point A.
On appelle distance du point A à la droite (D), la plus petite distance entre un point M de la droite (D) et le point A. On la note : d ( A ; (D)).

Théorème :

d ( A ; (D)) = AH où H est le projeté orthogonal de A sur (D).



En effet d'après le théorème de pythagore, pour tout M de (D) : AM ≥ AH

Théorème :

Dans le plan muni d'un repère orthonrmé : la distance du point A à la droite (D) d'équation ax + by + c = 0 est :


|ax_A + by_A + c| Valeur absolue de « l’équation de (D) » appliquée au point A.

Norme du vecteur normal de coordonnées ( a ; b ).

Remarque

si A ∈ (D), on retrouve bien d(A; (D))=0.

La démonstration de ce théorème fera l’objet d’un exercice.

 

7/ Equations cartésiennes de cercles et de sphères.

Dans le plan muni d’un repère orthonormé, considérons le cercle (C) de centre Ω et de rayon R.

Théorème : dans le plan muni d’un repère orthonormé :

L’équation cartésienne du cercle (C) de centre Ω et de rayon R est :


De même :

Théorème : dans le plan muni d’un repère orthonormé :

L’équation cartésienne d’une sphère (S) de centre Ω et de rayon R est :



Cette expression devant être développée pour obtenir une équation « réduite ».

Réciproquement, connaissant une forme réduite de l’équation, il faut être capable de retrouver les éléments caractéristiques du cercle ou de la sphère. C’est à dire : le centre et le rayon.