Cours maths 5ème

Nombres relatifs

A partir de situations concrètes, cette leçon introduit la notion de nombre relatif, de distance à zéro d’un nombre relatif, de nombres relatifs opposés. La deuxième partie de la leçon nous permet de comprendre comment comparer deux nombres relatifs.

Un problème d’étages

Jean entre dans l’ascenseur de l’immeuble et voit les boutons suivants :

 

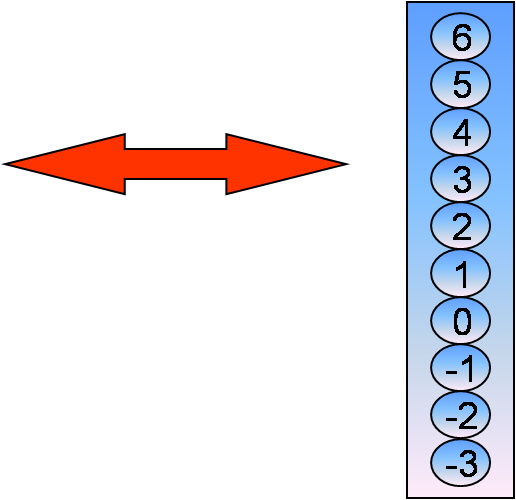Cabinet dentaire : 6ème étage

Cabinet médical : 2ème étage

Assurances tous risques : 1er étage

Gardien : rez de chaussée

Entrepôts : 1er sous-sol

Parking : 2ème et 3ème sous-sols

 

Quel bouton correspond au 6ème étage ?
...... 6

Quel bouton correspond au rez de chaussée ?
...... 0

Quel bouton correspond au 1er sous-sol ?
...... -1

Quel bouton correspond au 3ème sous-sol ?
...... -3

 

Un problème de dates

Comment, en histoire, écrit-on les dates suivantes ?

Victoire de César sur Vercingétorix en 52 avant J-C .......... - 52

Naissance de l’empereur Néron en 37 après J-C .......... 37

La république est proclamée à Rome en 509 avant J-C .......... - 509

Le mathématicien Euler est né en 1707 après J-C .......... 1 707

 

Les nombres relatifs : définitions

Les nombres utilisés pour repérer les différents étages, les différentes dates sont appelés: nombres relatifs

Les nombres précédés du signe « - » sont des nombres .......... négatifs.
Les nombres précédés du signe « + » ou d’aucun signe sont des nombres .......... positifs.
Les nombres positifs sont tous plus grands que zéro.
Les nombres négatifs sont tous plus petits que zéro.

 

Les nombres relatifs : remarque

Zéro est un nombre relatif; c’est le seul nombre relatif à la fois positif et négatif.

Un nombre négatif est toujours précédé du signe « – »
Devant un nombre positif on n’est pas tenu d’écrire le signe « + »

Les nombres relatifs sont parfois écrits entre des parenthèses.
4 et (+4) représentent le même nombre
-5 et (-5) représentent aussi le même nombre

 

Distance à zéro d’un nombre relatif

Sur une droite graduée, on associe à chaque point son abscisse qui est notée à l’aide d’un nombre relatif.
Si O est l’origine de la graduation et si M est un point de la droite, on appelle « distance à zéro » du nombre relatif abscisse du point M la longueur du segment [OM].

La distance à zéro du nombre 8 est 8.
La distance à zéro du nombre – 4 est 4.
La distance à zéro du nombre 3,57 est 3,57.
La distance à zéro du nombre – 2,8 est 2,8.

 

Nombres relatifs opposés

Deux nombres opposés sont deux nombres qui ont :
♦ la même distance à zéro
♦ des signes contraires

3,5 et – 3,5 sont des nombres relatifs opposés
– 5,82 et 5,82 sont des nombres relatifs opposés
0 est son propre opposé

 

Comparaison de deux nombres positifs

Le Mont Blanc a une altitude de 4 810 m.
L’Everest culmine à 8 848 m.

♦ Le sommet le plus haut est donc l’Everest.

En effet, on a 8 848 > 4 810.

De deux nombres positifs, le plus grand est celui qui a la plus grande distance à zéro.

 

Comparaison de deux nombres négatifs

On a relevé la température le 3 janvier à Paris et à Berlin. On a obtenu :
Paris : - 4° C Berlin : - 12°C
♦ C’est donc à Berlin que la température est la plus basse.

En effet, on a - 12

De deux nombres négatifs, le plus grand est celui qui a la plus petite distance à zéro.

Comparaison de deux nombres de signes différents

Voici les altitudes de deux lieux à la surface du globe :
Sommet du Kilimandjaro : 6 010 m
Fond du lac Ontario : - 118 m
♦ L’altitude du sommet du Kilimandjaro est donc supérieure à l’altitude du fond du lac Ontario.

En effet, on a - 118

Un nombre positif est toujours plus grand qu’un nombre négatif.