Cours de maths à partir de 9.90 €/heure
Cours maths 5ème
Le losange
Après avoir défini ce qu’est un losange, des activités guidées permettront de découvrir les propriétés de ses angles, l’existence d’axes de symétrie, d’un centre de symétrie, les propriétés de ses diagonales mais aussi que le losange est un parallélogramme . Il sera ensuite rappelé comment montrer qu’un quadrilatère est un losange à partir de ses côtés ou de ses diagonales.
Définition d'un losange
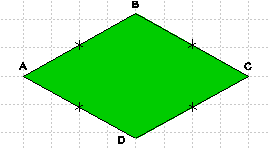 Le quadrilatère ABCD a quatre côtés de la même longueur : c’est un losange.
Le quadrilatère ABCD a quatre côtés de la même longueur : c’est un losange.
Définition :
Un losange est un quadrilatère qui a ses quatre côtés de la même longueur.
Un quadrilatère particulier :
 On admettra que le losange ABCD a ses côtés opposés parallèles ; c’est donc un parallélogramme.
On admettra que le losange ABCD a ses côtés opposés parallèles ; c’est donc un parallélogramme.
Propriété 1 :
Le losange est un parallélogramme.
Les angles du losange
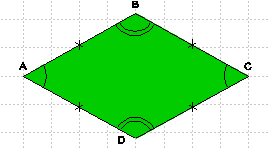 Le losange ABCD est un parallélogramme, donc :
Le losange ABCD est un parallélogramme, donc :
Les angles opposés ont la même mesure et les angles consécutifs sont supplémentaires.
Propriété 2 :
Le losange a ses angles opposés de même mesure et ses angles consécutifs supplémentaires.
Les diagonales du losange :
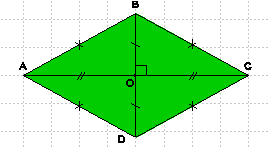 Le losange étant un parallélogramme, ses diagonales ont le même milieu O.
Le losange étant un parallélogramme, ses diagonales ont le même milieu O.
BA = BC donc B est un point de la médiatrice de [AC].
DA = DC donc D est un point de la médiatrice de [AC].
(BD) est donc la médiatrice de [AC].
On a donc (BD) perpendiculaire à (AC).
Propriété 3 :
Les diagonales du losange se coupent en leur milieu et sont perpendiculaires.
Les élements de symétrie du losange :
 Le losange étant un parallélogramme, le milieu O de ses diagonales est le centre de symétrie du losange.
Le losange étant un parallélogramme, le milieu O de ses diagonales est le centre de symétrie du losange.
Les triangles ABC et ADC sont isocèles et (BD) est la médiatrice de leur base.
(BD) est donc l’axe de symétrie de ces deux triangles.
Les triangles BAD et BCD sont isocèles et (AC) est la médiatrice de leur
base.
(AC) est donc l’axe de symétrie de ces deux triangles.
Propriété 4 :
un losange a deux axes de symétrie : ses diagonales;
il a un centre de symétrie : le point d’intersection de ses diagonales;
Reconnaître un losange.
 Le quadrilatère ABCD a 4 côtés de même longueur. ABCD est donc un losange.
Le quadrilatère ABCD a 4 côtés de même longueur. ABCD est donc un losange.
Propriété 5 :
Si un quadrilatère a 4 côtés de même longueur, alors ce quadrilatère est un losange.
 ABCD est un parallélogramme et AB = BC.
ABCD est un parallélogramme et AB = BC.
Ses côtés opposés sont donc de même longueur.
Ainsi, AB = DC et BC = AD.
Le parallélogramme ABCD a donc 4 côtés de même longueur ; c’est un losange.
Propriété 6 :
Si un parallélogramme a 2 côtés consécutifs de même longueur, alors ce parallélogramme est un losange.
 Dans le quadrilatère ABCD, les diagonales ont le même milieu O.
Dans le quadrilatère ABCD, les diagonales ont le même milieu O.
C’est donc un parallélogramme. AB = DC et BC = AD.
Les diagonales de ce parallélogramme sont perpendiculaires.
Dans le triangle ABC, (BO) est perpendiculaire au côté [AC] en son milieu; c’est donc sa médiatrice.
B est un point de la médiatrice de [AC], donc BA = BC.
Dans le triangle ADC, (DO) est perpendiculaire au côté [AC] en son milieu; c’est donc sa médiatrice.
D est un point de la médiatrice de [AC], donc DA = DC.
On a donc : AB = BC = CD = AD et ABCD est un losange.
Propriété 7 :
Si un quadrilatère a ses diagonales qui ont le même milieu et qui sont perpendiculaires, alors c’est un losange.
Cours complémentaires
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.
