Cours de maths à partir de 9.90 €/heure
Cours maths Terminale S
Généralités sur les suites
Ce module revient sur le programme de première : les différents types de suites, la monotonie, la convergence des suites, le tracé des termes d’une suite définie par récurrence.
1/ Types de suites : suite définie par une fonction
Type n ° 1 : suite définie par une fonction
Soit la suite définie par :
Il est possible pour cette suite de calculer immédiatement le terme u20 par exemple et plus généralement n’importe quel terme un de la suite.
Attention aux notations !
La notation un désigne le terme de rang n de la suite, il s’agit donc d’un nombre.
Tandis que la notation entre parenthèses : (un) désigne LA suite toute entière.
En effet, si on pose :
Ce type de suite peut être résumé par la formulation :
f étant une fonction définie sur l’ensemble des réels positifs.
Représentation des termes d’une suite définie par une fonction :
Reprenons notre exemple :
On peut à l’aide de la représentation de f sur les réels positifs tracer les termes de la suite :
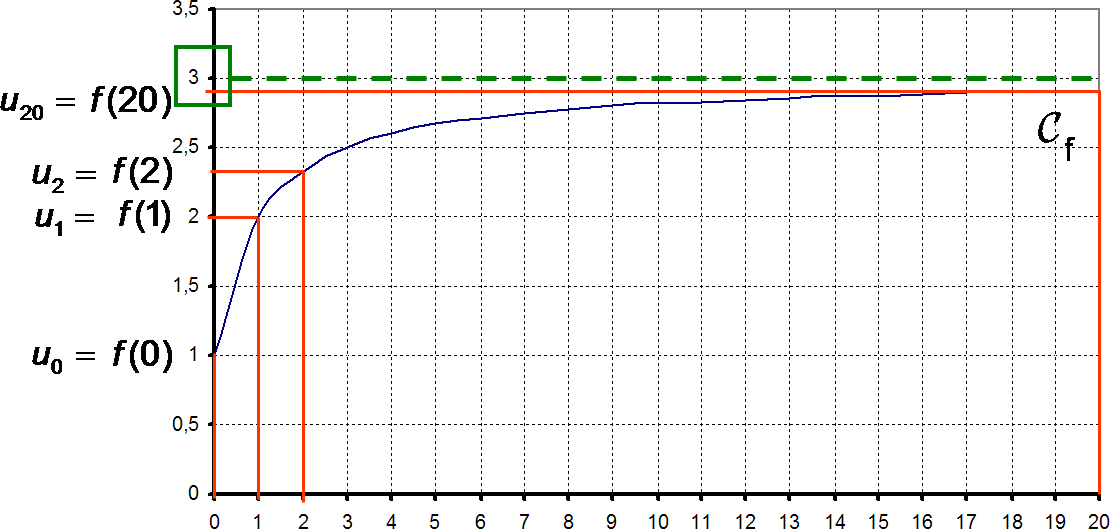
Graphiquement, il est clair que pour ce type de suite :
ceci est vrai que si f admet en une limite finie ou infinie.
Remarques :
1° ) Pour ce type de suites, on va donc gérer la recherche de la limite de (un) comme on gérerait la recherche de la limite de f en , mais en utilisant n comme variable.
2° ) Une suite ne pouvant avoir de limite qu’en , on notera pour simplifier :
Si lim un est un nombre fini , on dira que la suite converge vers
,
ou encore qu’elle est convergente.
Dans le cas contraire, on dira que la suite diverge,
ou encore qu’elle est divergente.
Etudier la convergence d’une suite, c’est donc chercher sa limite en ,
et déterminer en fonction du résultat si la suite converge ou diverge.
Attention !
Une suite divergente ne tend pas forcément vers l’infini.
Exemple : un = (-1)n oscille et n’a de limite ni finie, ni infinie.
Type n ° 2 : suite définie par récurrence
Soit la suite définie par :
Il est alors a priori impossible de calculer immédiatement le terme u20 , par exemple.
Pour atteindre u20, il faut d’abord calculer les 19 termes qui le précèdent.
La relation de récurrence peut être résumée par la formulation :
f est appelée fonction associée à la suite.
Remarque : il existe des relations de récurrence liant plus de deux termes consécutifs et qui ne se ramènent donc pas à ce cas.
Représentation des termes d’une suite définie par récurrence :
On peut donc à l’aide de la courbe de f, trouver u1 en traçant l’image de u0
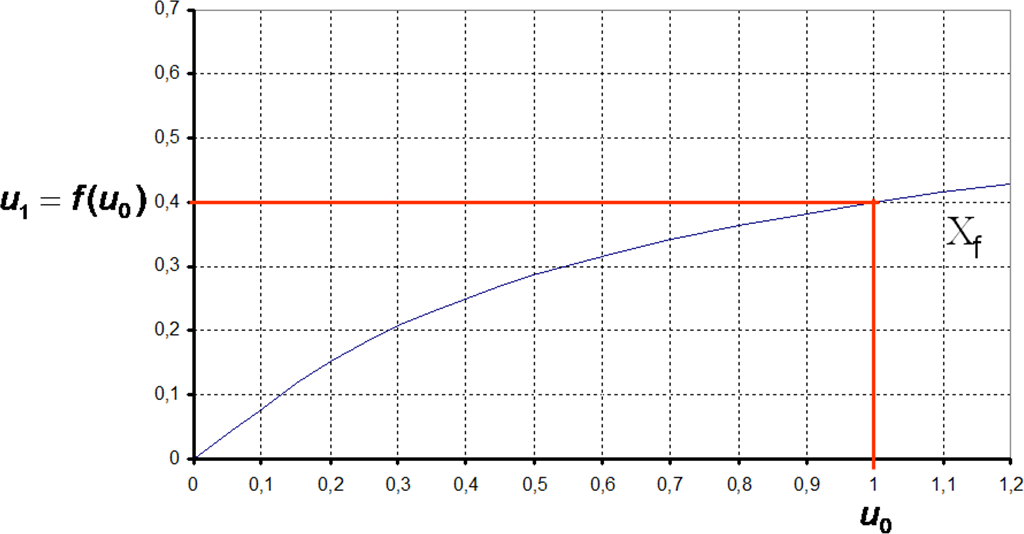
Pour tracer l’image de u1, il faut maintenant le ramener sur l’axe des abscisses à l’aide de la première bissectrice d’équation : y = x.
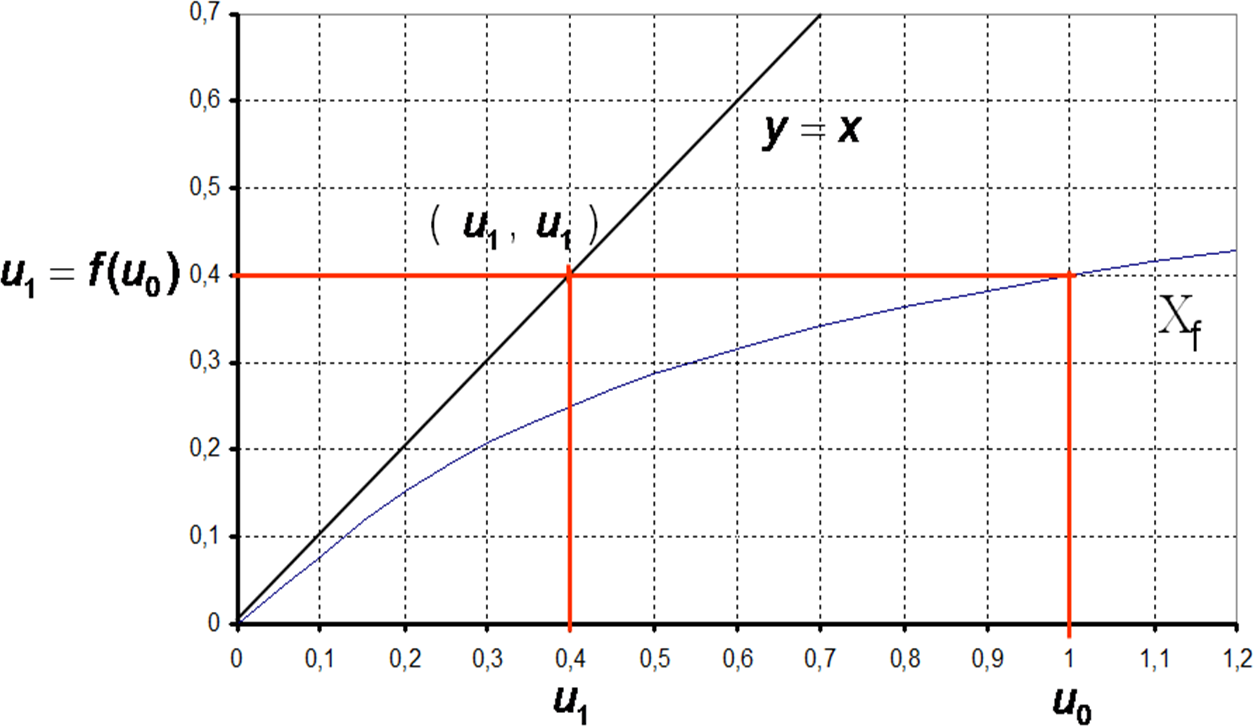
On continue ainsi l’opération …
Et une fois que l’on a bien compris le fonctionnement,
il n’est même plus besoin de pousser le trait jusqu’à l’axe des ordonnées.
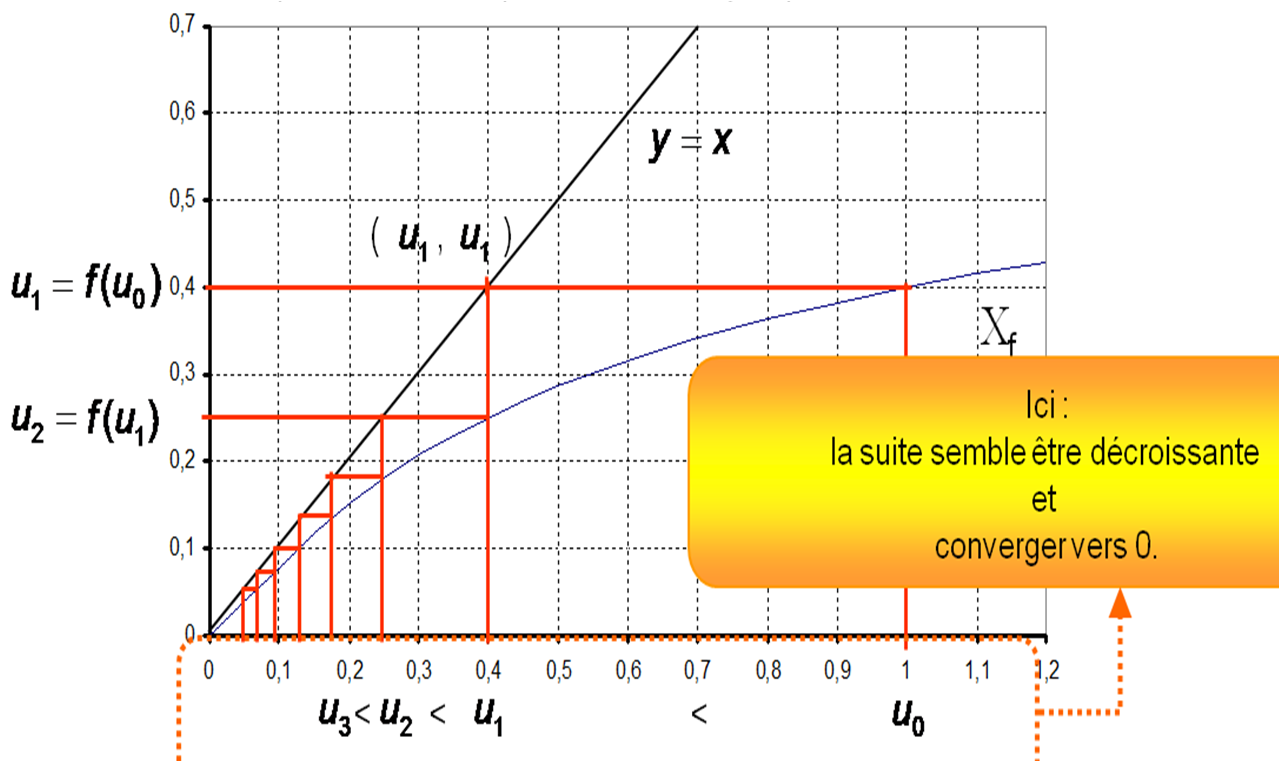
Théorème :
Soit une fonction f définie sur un intervalle I et soit (un) une suite vérifiant : pour tout n :
Si (un) converge vers
et si f est continue en
alors
vérifie : f (
) =
Pour trouver les valeurs possibles de
, il faut donc résoudre l’équation : f(x) = x
Graphiquement :
Un point dont le couple de coordonnées est de la forme ( ; f (
)) est sur la courbe de f.
Et comme f (
) =
, le couple peut aussi être écrit
(
;
) donc ce point est également sur la droite d’équation y = x, qui est la première bissectrice.
Si (un) converge vers
et si f est continue en
alors
est l’ abscisse d’un des points d’intersection entre la courbe de f et la première bissectrice.
illustration :
Soit la suite (un) définie par la relation :
Voici la représentation de sa fonction associée définie par :
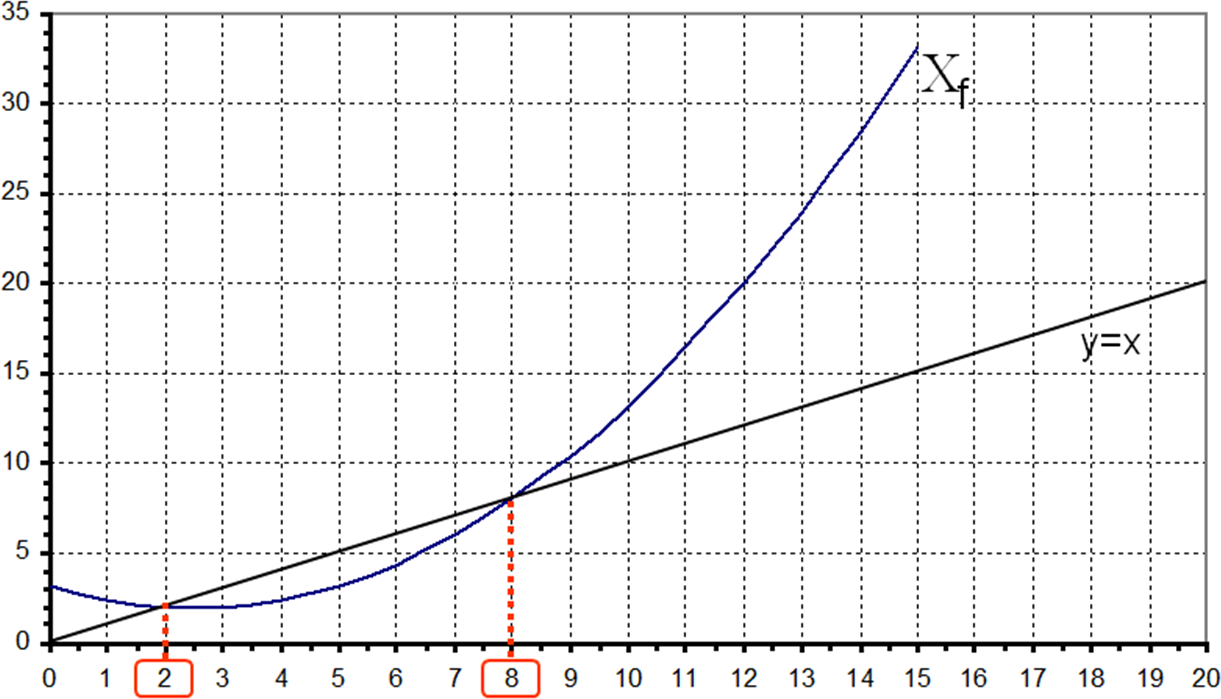
Graphiquement, on trouve que les deux valeurs possibles pour la limite de (un) sont : 2 et 8.
Mais attention, rien ne prouve que la suite converge vers une de ces valeurs.
.png)
Tout dépend de la valeur du premier terme :
Mais attention ici à ne pas émettre une conjecture trop rapide !
En effet, si on continuait le tracé,
on remarquerait sur un graphique plus précis
que le terme suivant devient inférieur à 2.
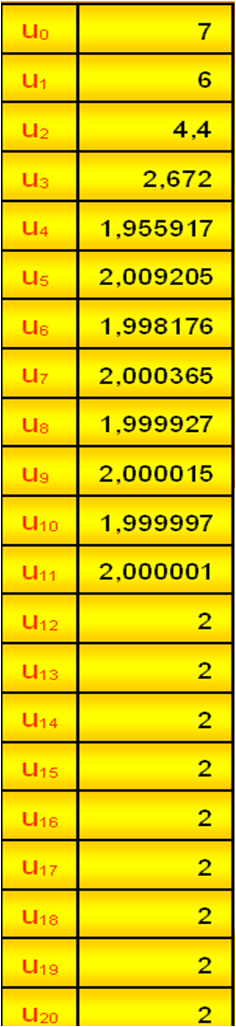
Il est toutefois possible de confirmer l’hypothèse de convergence
à l’aide d’un tableur.
Cependant, quelle que soit la méthode de conjecture utilisée, seule une démonstration mathématique constitue une preuve.
2/ Sens de variation d’une suite
Etudier le sens de variation, les variations ou encore la monotonie d’une suite, c’est comparer deux termes consécutifs quelconques de cette suite.
Si pour tout n : un+1 > 1 la suite est dite croissante et on note : (un)
Si pour tout n : un+1 (un)
Si pour tout n : un+1 = 1 la suite est dite constante et on note : (un)
Remarques :
1) Il se peut que : un+1 > 1 ne soit pas vraie pour tout n mais seulement
à partir d’un certain rang. On dira alors que la suite est croissante à partir de ce rang.
2) En toute rigueur :
si pour tout n : un+1 > 1 on devrait dire que la suite est strictement croissante.
La dénomination croissante s’appliquant au cas :un+1 > 1
Mais rédacteurs de livres comme rédacteurs de sujets de BAC
sont assez peu rigoureux sur le sujet.
Techniques pour comparer un+1 et un :
Technique n °1 : technique de base valable pour tout type de suite.
On étudie le signe de la différence : un+1 - un
Par exemple : si pour tout n : un+1 - un > 0 alors un+1 > un et donc : (un)
Technique n °2 : technique valable uniquement si le terme général est de signe constant.
Technique n °3 :
Si un = f(n) alors le sens de variation de (un)est le même que celui de f sur [0 ; ]
Il suffira alors d’étudier les variations de f sur cet intervalle, à l’aide par exemple de la dérivée.
Remarque
: les élèves ont souvent envie d’appliquer cette technique à la fonction associée à une suite définie par récurrence.
Voyons graphiquement si cette idée est valable.
Exemple :
Voici la courbe de la fonction associée définie par :
Cette fonction affine est croissante sur R donc a fortiori sur [0 ; ]
.png)
Conclusion :
Bien que f soit croissante sur [0 ; ] selon la valeur de son premier terme, la suite, elle, peut être croissante ou décroissante.
3 / Suite majorée, minorée ou bornée
Soient M et m deux nombres réels. Et (un) une suite de nombres réels.
* (un) est dite majorée par M si pour tout n : un * (un) est dite minorée par m si pour tout n : un > m
* (un) est dite bornée si elle est à la fois majorée et minorée.
Autrement dit, s’il existe M et m réels tels que pour tout n : m
Remarque :
Ces propriétés peuvent aussi n’être vraies qu’à partir d’un certain rang.
Techniques que l'on peut utiliser pour arriver à démontrer ce type d'inégalités:
- Etude du signe d’une différence.
Méthode la plus sûre
- Manipulation d’inégalités.
Méthode très risquée souvent source d’erreurs
- Etude de la fonction de définition.
- Utilisation d’un raisonnement par récurrence.
Technique dont l’étude fait l’objet d’un autre module
4 / Limite d’une suite majorée, minorée ou bornée.
Soit (un) une suite de nombres réels convergente.
Si pour tout n, ou si à partir d’un certain rang : un alors : lim un
Attention !
Il est à noter que même si tous les termes de la suite sont strictement inférieurs à M, la limite de la suite peut, elle, être égale à M.
En effet, si par exemple : alors, pour tout n non nul : un - or : lim un
Si pour tout n, ou si à partir d’un certain rang : un
alors : lim un
et conséquence des deux théorèmes :
Si pour tout n, ou si à partir d’un certain rang : m alors : m
Remarque:
Ces résultats sont en particuliers utiles dans la recherche de la limite L d’une suite définie par récurrence, et souvent nécessaires pour savoir si l’on peut appliquer le théorème donnant f(L) = L
5 / Cas particulier n° 1 : cas des suites arithmétiques
Il existe certaines suites qui bien que définies par récurrence
peuvent se ramener à une suite définie par une fonction.
C’est le cas des suites arithmétiques.
(un) est dite
arithmétique si la relation de récurrence qui la définit est du type :
un+1 = un + r
r étant une
constante, et donc indépendante de n.
r est appelé la
raison de la suite.
Pour montrer qu’une suite est arithmétique,
il faut donc montrer qu’il existe un nombre r indépendant de n tel que :
Quel que soit n : un+1 = un + r
Autrement dit, il faut montrer que la différence : un+1 - un est constante.
Cette différence étant alors la raison de la suite.
Pour montrer qu’une suite
n’est pas arithmétique,
il suffit de prouver que sur les premiers termes de la suite, cette différence n’est pas constante.
Attention !
Ce n’est pas parce que sur les premiers termes, la différence est constante qu’elle le sera forcément sur les termes suivants.
Trouver une différence constante sur les premiers termes ne suffit donc pas à prouver que la suite est arithmétique.
Recherche de la formule permettant de calculer directement le terme général : un
.png)
*
Expression du terme général en fonction de n, en partant de
Remarque :
Une démonstration rigoureuse de cette formule se ferait par récurrence.
Il est donc maintenant possible de calculer immédiatement n’importe quel terme.
La suite est devenue du type : un = f(n)
*
Expression du terme général en fonction de n, en partant de
L’erreur classique est de prendre n au lieu de (n-1).
* Expression du terme général en fonction de n, en partant de
Cette formule résume à elle seule les trois cas mais étant donné que l’on rencontre très souvent les deux premiers cas il est conseillé de les connaître directement.
Remarque :
Dans un exercice, donner une de ces trois formules c’est répondre à une question du type :
- en déduire l’expression du terme général de la suite.
- Ou encore, donner le terme général de la suite en fonction
de n.
- Questions dont les élèves ont souvent du mal à saisir le sens.
Variations d’une suite arithmétique :
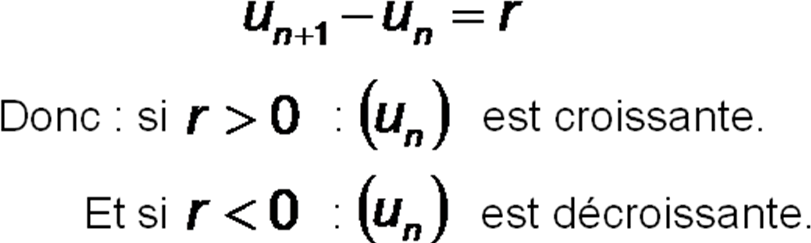
Limite d’une suite arithmétique :
On peut ici considérer la chose du point de vue de la définition d’une limite :
Par exemple : si r > 0 , comme un+1 = un + r :
Quel que soit A > 0 ( aussi grand que l’on veut ), il existe un rang n0 tel que :
pour tout n > n0 : un > A
d'où : lim un =
Ou on peut tout simplement, utiliser les limites de fonction :
Somme des termes d’une suite arithmétique :
Exemple : soit (un) suite arithmétique de premier terme u0 = -2 et de raison r = 4.
Heureusement, il existe une formule pour trouver directement ce résultat sans calculer tous les termes de la somme :
S = Moyenne des termes extrêmes x Nombre de termes
6 / Cas particulier n° 2 : cas des suites géométriques
Les suites géométriques aussi, bien que définies par récurrence
peuvent se ramener à une suite définie par une fonction.
(un) est dite
géométrique si la relation de récurrence qui la définit est du type :
un+1 = un x q
q étant une
constante, et donc indépendante de n.
q est appelé la
raison de la suite.
* Pour montrer qu’une suite
est géométrique,
il faut donc montrer qu’il existe un nombre q indépendant de n tel que :
Quel que soit n : un+1 = un x q
Autrement dit, il faut montrer que le quotient : est constant.
Ce quotient étant alors la raison de la suite, d’où la notation « q ».
* Pour montrer qu’une suite n’est pas géométrique,
il suffit de prouver que sur les premiers termes de la suite, ce quotient n’est pas constant.
Attention !
Ce n’est pas parce que sur les premiers termes, le quotient est constant qu’il le sera forcément sur les termes suivants.
Trouver un quotient constant sur les premiers termes ne suffit donc pas à prouver que la suite est géométrique.
Recherche de la formule permettant de calculer directement le terme général : un
.png)
*
Expression du terme général en fonction de n, en partant de
Il est donc maintenant possible de calculer immédiatement n’importe quel terme.
La suite est devenue du type : un = f(n)
*
Expression du terme général en fonction de n, en partant de
L’erreur classique est de prendre n au lieu de (n-1).
* Expression du terme général en fonction de n, en partant de
Signe du terme général d’une suite géométrique :
un = u0 x qn
Si q > 0 : un est du signe de u0
Si q
(Il est de même que u0 si n est pair de signe opposé à u0 si n est impair)
Variations d’une suite géométrique :
Uniquement dans le cas où un est de signe constant, c’est à dire, cas q > 0
Remarque :
Ces résultats généraux ne sont pas à apprendre mais à savoir retrouver sur l’étude de cas particuliers.
Si (un) est géométrique de premier terme u0 et de raison q alors : un = u0 x qn
D’où : lim un = u0 x lim qn
Il est donc important de connaître les valeurs possibles de lim qn
* Si q > 1
Quel que soit a > 0 ( aussi grand que l’on veut ), il existe un rang n0 tel que :
pour tout n > n0 : qn > a
Donc tout intervalle ]a ; [ contient tous les termes de la suite à partir d’un certain rang.
d'où lim qn= et (un) diverge
* Si q = 1 , alors pour tout n : qn = 1
d’où : lim qn = 1
Et (un) converge vers u0

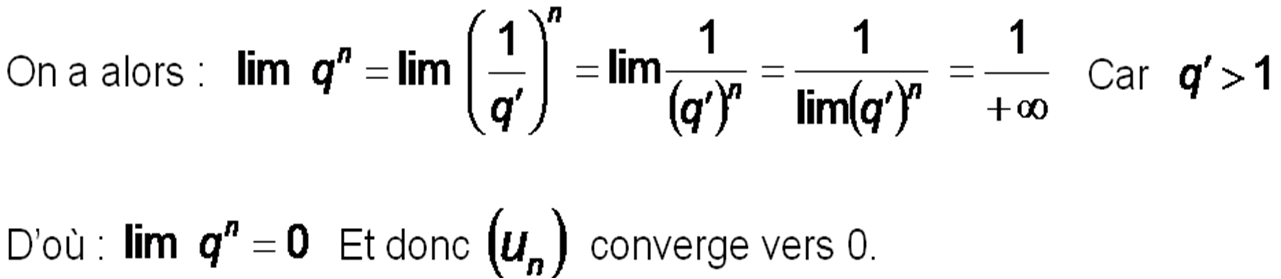
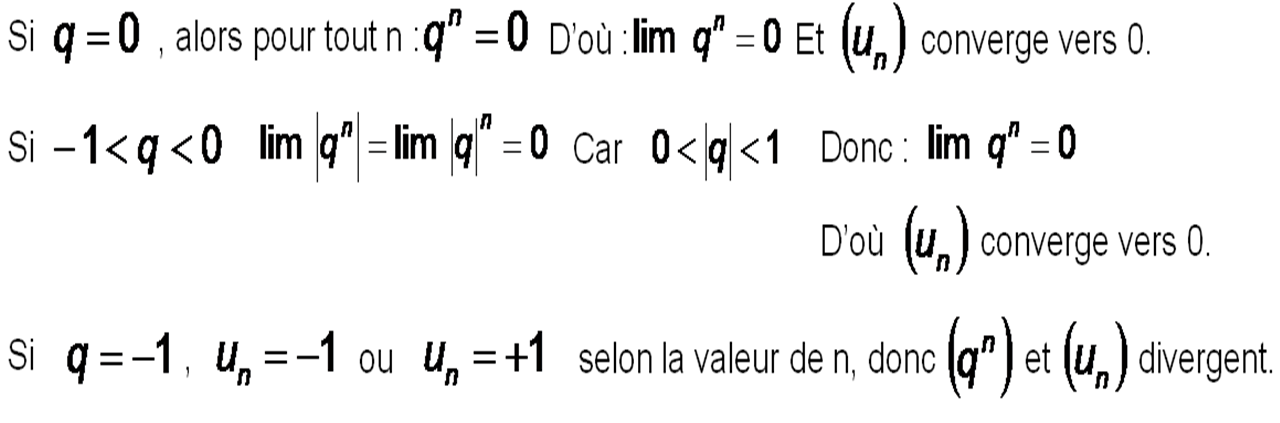
Limites d'une suite géométrique :
Si un = u0 x qn
lim un = u0 x lim qn donc :
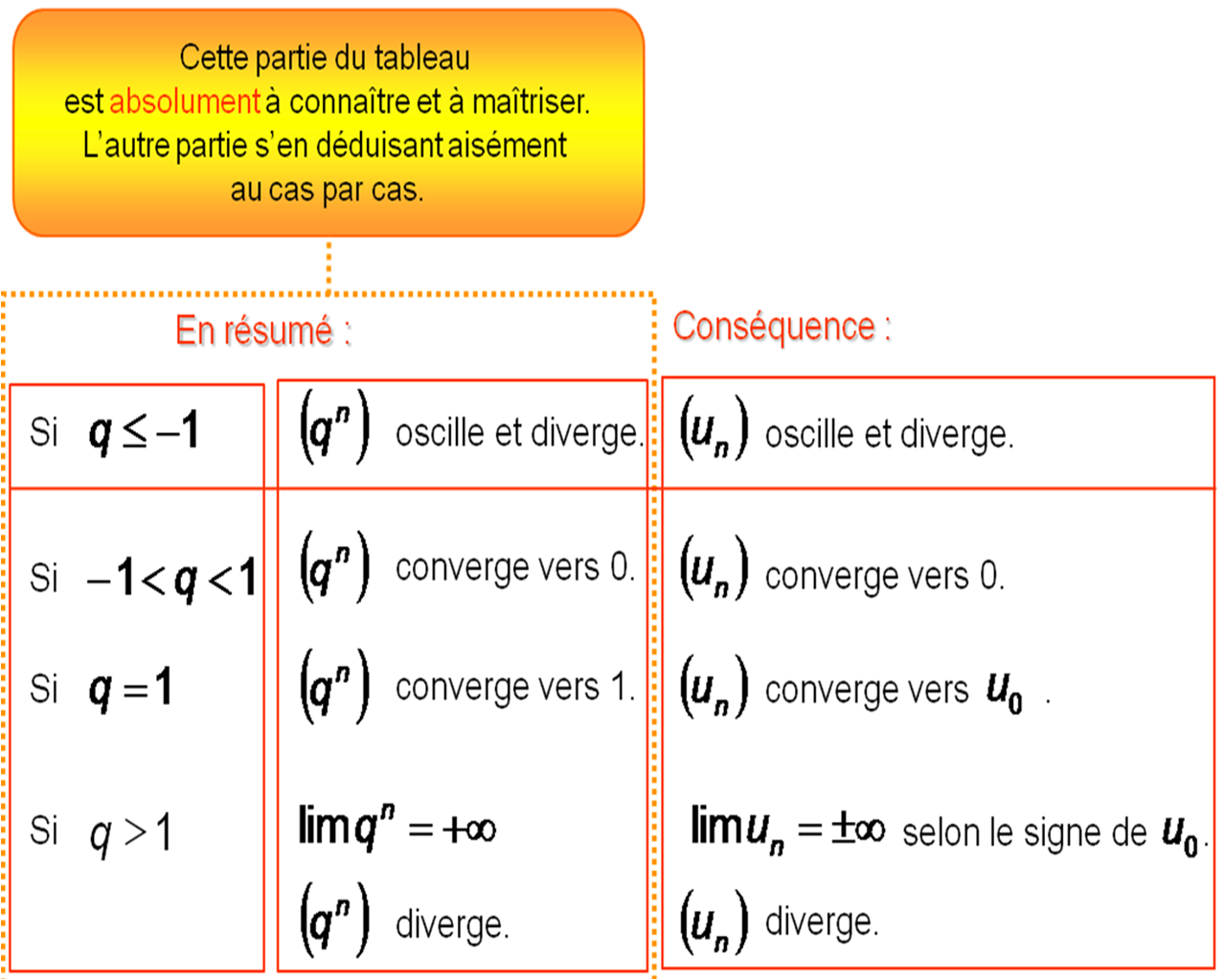
Somme des termes d’une suite géométrique :
Exemple : soit (un) suite géométrique de premier terme u0 = 3 et de raison q = 2.
Soit S = u2 + u3 + u4 + u5 + u6
.png)
Heureusement, il existe une formule pour trouver directement ce résultat sans calculer tous les termes de la somme :
S = Premier terme de la somme x
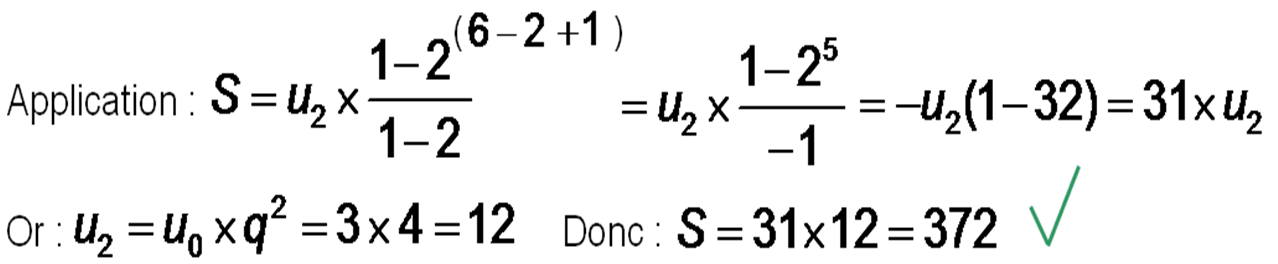
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.