Cours maths Terminale S

Surfaces de l'espace : Généralités et Fonctions de deux variables

Fonctions de deux variables

 

1/ Fonction de deux variables : définition

Définition

Soient I et J deux intervalles de ℝ et soit ( x ; y ) couple de réels appartenant respectivement à I et à J.

On appelle fonction numérique de deux variables réelles, toute fonction, qui au couple ( x ; y ) associe un réel noté f(x ; y).

Exemple n° 1 :

f(x;y) = −2x + y + 3

Exemple n° 2 :

f(x;y) = x² + 3y

 

2/ Fonction de deux variables : représentation

Représentation d’une fonction de deux variables :

La représentation d’une fonction f de deux variables est la surface constituée de l’ensemble des points M de l’espace de coordonnées ( x ; y ; z ) avec z = f ( x ; y ).
La surface (S) a alors pour équation : z = f (x ; y ).

Exemple n° 1 :

f(x;y) = −2 + y + 3

(S) a alors pour équation :
z = −2x + y + 3

(S) est donc le plan d’équation :
2x − y + z = 0

Voici la représentation de cette surface à l’aide d’un tableur-traceur :

Les x et y étant pris dans l’intervalle [ 0 ; 10 ]

Exemple n° 2 :

f(x;y) = x² + 3y

(S) a alors pour équation :
z = x² + 3y

Voici la représentation de cette surface à l’aide d’un tableur-traceur :

Les x étant pris dans l’intervalle [ -5 ; 5 ] et les y dans l’intervalle [ -8 ; 8 ].

 

2/ Lignes de niveau

Définition

soit une surface (S) et un réel k donné.

On appelle ligne de niveau k de la surface (S),la courbe obtenue par section de la surface (S) par le plan d’équation z = k.

Exemple n° 1 :

f(x;y) = −2x + y + 3

La ligne de niveau 5 de la surface (S) est ici une droite. Elle représente sur le graphique la frontière entre les zones roses et violettes.

Son système d’équation est :

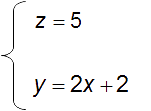
Dans le plan d’équation z = 5,la ligne de niveau 5 a donc pour équation : y=2x+2

Exemple n° 2 :

f(x;y) = x² + 3y

En superposant dans un même plan différentes lignes de niveaux,on peut avoir une idée de la surface :

Remarque

Ce principe de représentation du relief à l’aides des lignes de niveau est en particulier utilisé en cartographie.

Et de même qu’une fonction d’une variable peut n’être connue que par la donnée de sa courbe,une fonction de deux variables peut n’être connue que par la donnée de sa surface ,ou par la donnée des projections des intersections de sa surface par des plans parallèles entre eux.

La fonction est alors connue par ce que l’on nomme ses abaques. En particulier, si ces plans sont des plans parallèles au plan (xOy), c’est à dire d’équation de type z=k, les abaques sont la projection des lignes de niveau.

Exemples de lecture d’abaques :

M ( 3 ; -3 ) est à la frontière des zones jaune et turquoise.

Il est donc sur la ligne de niveau 0.

D’où : f ( 3 ; -3 ) =0.

En effet, on sait ici que : f(x;y) = x² + 3y

Et, on a bien : f(3;−3) = 9 −9 = 0

M ( -4 ; 6 ) est dans la zone bleue
Donc : 30 ≤ f(−4;6) ≤ 40

En effet : f(−4;6) = 16 + 18 = 34

 

3/ Equations de plans particuliers

Comme on vient de le voir, pour appréhender la nature d’une surface , il peut être intéressant de chercher ses intersections avec des plans de l’espace.

Aussi, passons en revue les équations des plans les plus fréquemment rencontrés :
Rappelons tout d’abord que tout plan de l’espace
admet une équation cartésienne du type: ax + by + cz = 0

Démonstration

Soit (P) parallèle à (Ox) d’équation ax + by + cz + d =0.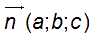
est une vecteur normal à (P) et 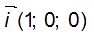est un vecteur directeur de (P).

Donc : et sont orthogonaux d’où : 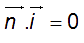.Soit : a x 1 + b x 0 + c x 0

Par conséquent a=0 et (P) a une équation du type : by + cz + d = 0

plan parallèle - plan parallèle à l'axe (Ox) : by + cz + d =0

plan parallèle - plan parallèle à l'axe (Oy) : ax + cz + d =0

plan parallèle - plan parallèle à l'axe (Oz) : ax + by + d =0

Remarque

ces formules sont très simples à retenir.
En effet, si (P) est parallèle à (Ox) alors son équation n’a pas de x et ainsi de suite…

 

4/ Surface de révolution

Définition

soit une surface (S) et une droite (D). (S) est une surface de révolution d’axe de révolution (D) si : les sections de (S) par des plans perpendiculaires à (D) sont des cercles de centre situé sur (D).

Vocabulaire

Ces cercles sont appelés les parallèles à (S).

Exemple

1° Une sphère est une surface de révolution d’axe toute droite passant par son centre.
2° Cette portion de cône est une surface de révolution d’axe de révolution, l’axe (Oz).

Une parallèle de (S)

Génération d’une surface de révolution :

La rotation d’une courbe autour d’une droite fixe engendre une surface de révolution.
Cette courbe est appelée une génératrice.

Vocabulaire

La section d’une surface de révolution par un demi-plan de frontière l’axe de révolution est appelée une méridienne.

Propriété

Toute méridienne est une génératrice de la surface de révolution.

cette méridienne, qui est ici une droite, engendre la surface de révolution, par rotation autour de l'axe (Oz)

 

5/ Les paraboloïdes : paraboloïde elliptique

Définition

Soit une réel k donné.

Une surface (S) d’équation : z = k(x² + y²) est appelée un paraboloïde elliptique.

Exemple

Pour k=1, traçons la représentation de f définie par : . f(x ; y) = x² + y²

Propriété

Tout paraboloïde elliptique d’équation : z = k(x² + y²) est une surface de révolution d’axe (Oz).

En effet, si on trace les lignes de niveau de (S) :ce sont des cercles dont le centre est sur (Oz).

Démonstration

Soit le plan (P) perpendiculaire à (Oz).
Il est parallèle au plan (xOy) donc a une équation du type : z = a.


Si a Si a = 0 : le point O ( 0 ; 0 ; 0 ) est l’unique solution.

Si a > 0 : l’intersection est le cercle contenue dans (P) de centre A ( 0 ; 0 ; a) et de rayon .

Propriété

L’intersection de (S) par un plan parallèle à (xOz) ou (yOz) est une parabole d’axe parallèle à (Oz).

Remarque

Plus généralement,toute intersection de (S) avec un plan parallèle à l’axe (Oz) est une parabole d’axe parallèle à (Oz).

Démonstration sur un exemple

Prenons (S) d’équation : z = x² + y² et cherchons son intersection avec (P) : x = -3.


On a donc : z = g(y) avec g(y) = y² + 9
C’est une fonction du second degré, donc sa représentation est une parabole.
Le tableur grapheur nous donne le tracé suivant dans le plan (P) :

Remarque

Plus généralement, toute intersection de (S) avec un plan parallèle à l'axe de (Oz) est une parabole d'axe parallèle à (Oz)

 

5/ Les paraboloïdes : paraboloïde hyperbolique

Définition

Soit un réel k donné.

Une surface (S) d’équation : z = kxy est appelée un paraboloïde hyperbolique d’axe (Oz).
Pour k=1, traçons la représentation de f définie par : f(x ; y) = xy

Propriété

Les lignes de niveau non nulles sont des hyperboles.

Démonstration

Soit le plan (P) d’équation : z = a.


L’intersection est alors égale aux axes (Ox) et (Oy).


L’intersection est alors une hyperbole. D’où le qualificatif d’hyperbolique.

Propriété

L’intersection de (S) par un plan parallèle à (xOz) ou (yOz) est une droite.

Démonstration sur un exemple
Prenons (S) d’équation : z = xy et cherchons son intersection avec (P) : x = 2.


C’est une fonction affine ( linéaire ), donc sa représentation est une droite.
Le tableur grapheur nous donne le tracé suivant dans le plan (P) :

Propriété

L’intersection de (S) par un plan parallèle à (Oz) est soit une parabole soit une droite.
Voyons sur exemple le cas d’un plan parallèle à (Oz ) mais non parallèle aux plans de base :
Prenons (S) d’équation : z = xy et cherchons son intersection avec (P) : x+y=0



C’est une fonction du second degré donc sa représentation est une parabole.
D’où le nom de paraboloïde.

 

6/ Avis au lecteur

Peu d’exercices du BAC S portent sur ce module.
Sur les dernières années, un seul exercice sur ce sujet a été posé.
Et comme il est plutôt difficile, il ne figure pas dans ce module de niveau 1.

Par contre, ce module fait souvent l’objet d’exercices de spécialité pour le BAC ES.
Intéressants et d’un niveau de difficulté très correct, nous avons choisi d’en utiliser certains dans la partie exercices.