Cours maths 5ème

Construction d'un triangle

Ce chapitre rappelle les différentes façons de construire un triangle : en connaissant les longueurs de ses 3 côtés ; en connaissant la longueur de 2 côtés et la mesure de l’angle formé par ces deux côtés ; en connaissant la longueur d’un côté et les mesures des angles situés de part et d’autre de ce côté.

 

Éléments de base d’un triangle

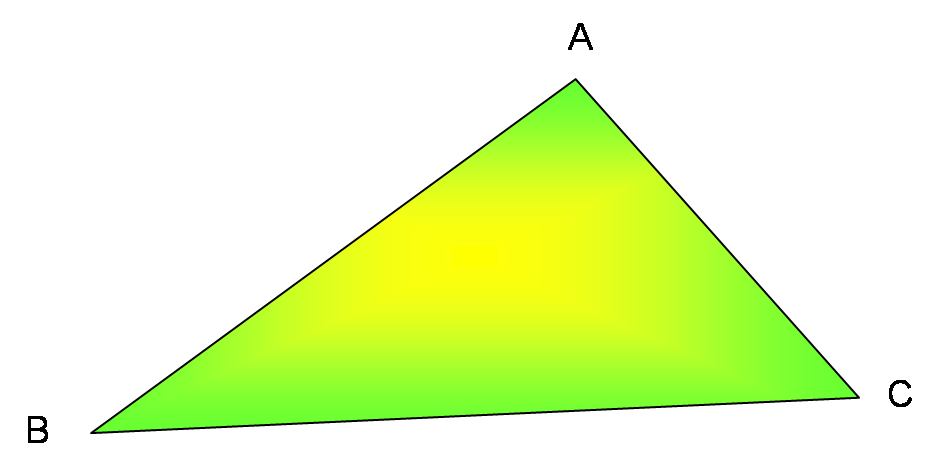Dans le triangle ABC,

On a 3 côtés : [AB], [AC] et [BC].

On a 3 angles : 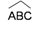, 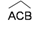et

 

 

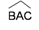
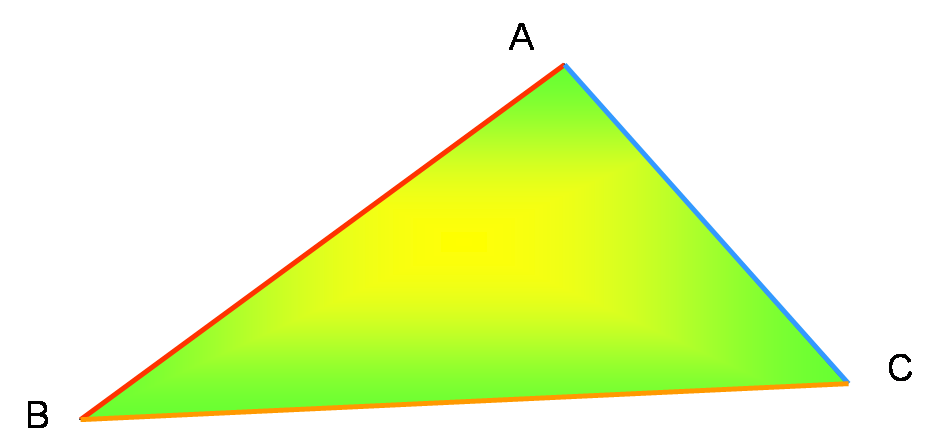On connaît les longueurs de 3 segments : [AB], [AC] et [BC]

D'après l'inégalité triangulaire, si la plus grande longueur est inférieure à la somme des deux autres, alors on peut construire un triangle ABC.

Voyons comment réaliser cette construction.

 

Construction d'un triangle en utilisant la règle et le compas

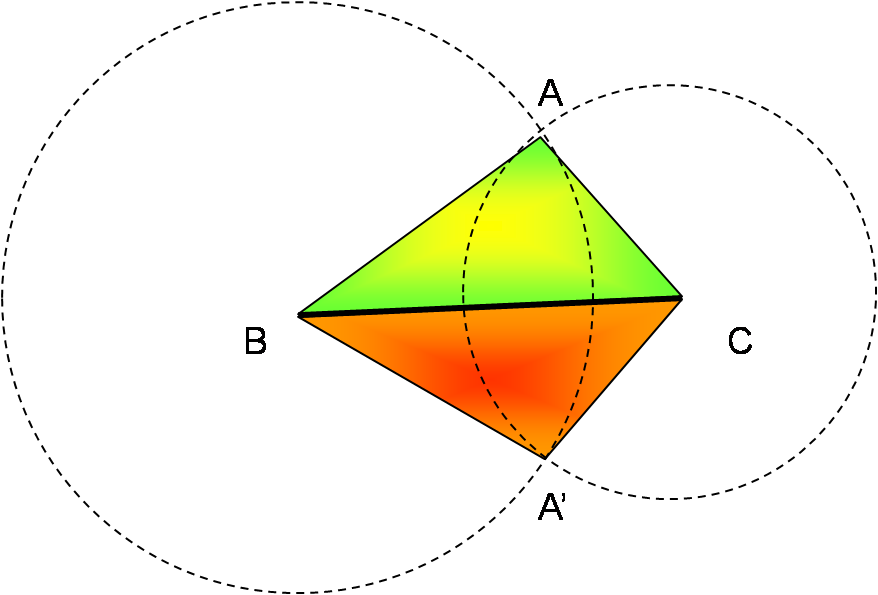On connaît les longueurs des 3 côtés : [AB], [AC] et [BC].

• On commence par tracer un des côtés, par exemple [BC].
• On trace alors le cercle de centre B et de rayon AB.
• Puis celui de centre C et de rayon AC.
• Les deux cercles se coupent en deux points ; l’un est le point

A cherché, l’autre son symétrique A’ par rapport à la droite (BC).

On peut donc construire deux triangles :

Le triangle ABC et le triangle A’BC.

 

Construction d'un triangle en utilisant la règle et le rapporteur (1er cas)

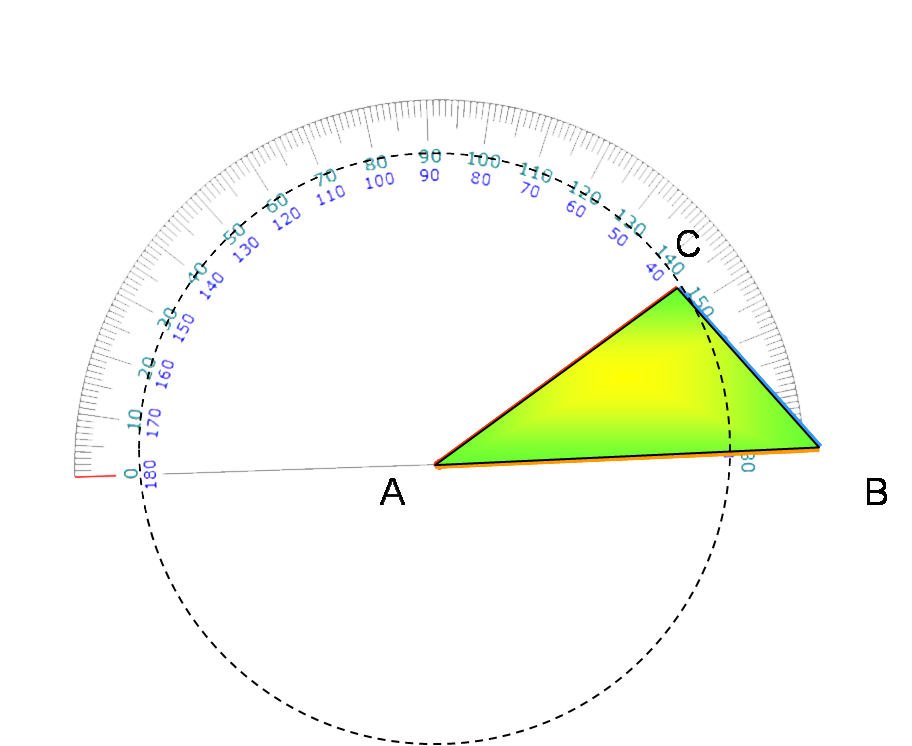On connaît les longueurs de 2 côtés [AB], [AC] et la mesure de l’angle qu’ils forment.

On commence par tracer un des côtés, par exemple [AB].
On trace alors le cercle de centre A et de rayon AC.
Puis on construit, à l’aide du rapporteur, un angle de sommet A, dont un des côtés est la demi-droite [AB) et dont la mesure est celle de .
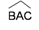Le cercle et la demi-droite se coupent en un point : C.
On trace alors le 3ème côté : [BC].

On construit ainsi le triangle ABC.

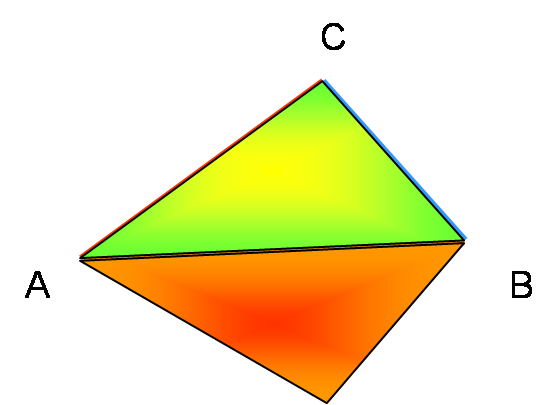On peut aussi obtenir un deuxième triangle symétrique du premier par rapport à la droite (AB).

On peut donc construire les triangles ABC et A’BC.

Il suffit de construire l’angle de l’autre côté du segment [AB].

 

Construction d'un triangle en utilisant la règle et le rapporteur (2ème cas)

On connaît la longueur du côté [AB] du triangle ABC et la mesure des angles dont il est un côté.
AB = 6,7 cm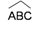
= 50°
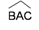= 65°

On trace d’abord [AB] tel que AB = 6 cm.
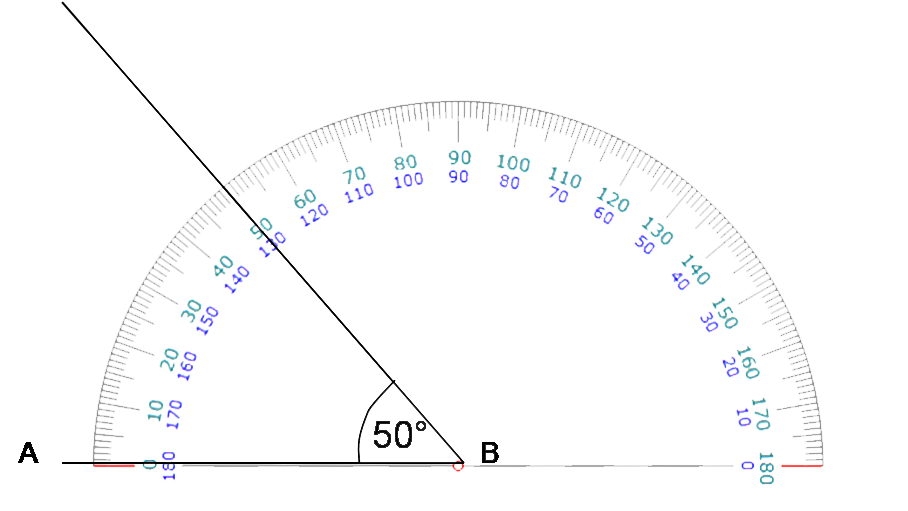
À l’aide du rapporteur, on construit alors un angle de 50° de sommet B et dont [BA) est un côté.

 

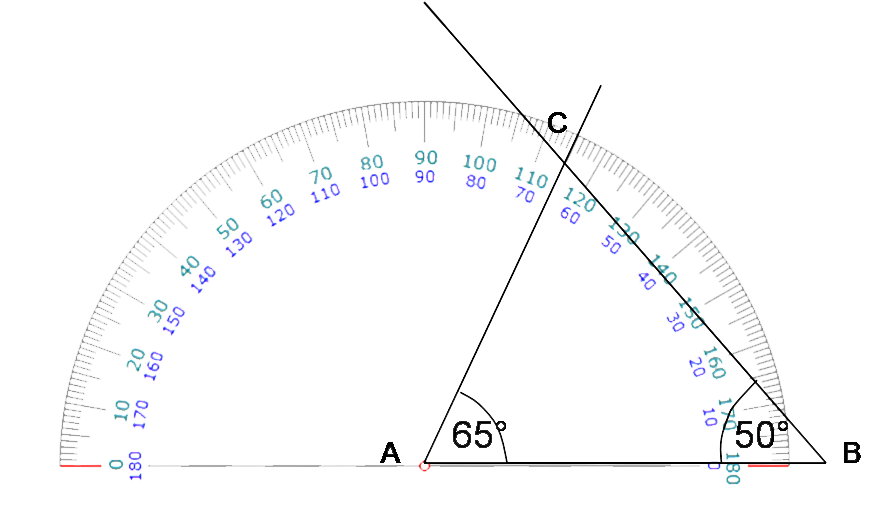Ensuite, avec le rapporteur, on construit de la même manière un angle de 65° de sommet A et dont [AB) est un côté.

C est alors le point d’intersection des deux demi-droites obtenues.

On obtient ainsi le triangle ABC.