Cours maths Terminale S

Cônes et cylindres illimités

Ce module revient sur tout le programme de première concernant les cônes et cylindres illimités.

 

1/ Equations de plans particuliers

Pour appréhender la nature d’une surface de l’espace, il est souvent intéressant de chercher ses intersections avec des plans de l’espace.

Aussi, passons en revue les équations des plans les plus fréquemment rencontrés :

Rappelons tout d’abord que tout plan de l’espace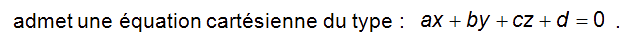

- plan parallèle au plan (xOy) :
z = a

- plan parallèle au plan (yOz) :
x = b

- plan parallèle au plan (xOz) :
y = c

Démonstration

Soit (P) parallèle à (Ox) d’équation ax + by + cz + d = 0.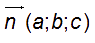
est une vecteur normal à (P) et 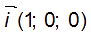est un vecteur directeur de (P).

Donc : et sont orthogonaux d’où : Soit : a×1 + b×0 + c×0 = 0 .

Par conséquent a=0 et (P) a une équation du type : by + cz + d = 0

- plan parallèle à l’axe (Ox) :
by + cz + d = 0

- plan parallèle à l’axe (Oy) :
ax + cz + d = 0

- plan parallèle à l’axe (Oz) :
ax + by + d = 0

Remarque

ces formules sont très simples à retenir.
En effet, si (P) est parallèle à (Ox) alors son équation n’a pas de x et ainsi de suite…

 

2/ Surface de révolution

Définition

soit une surface (S) et une droite (D).

(S) est une surface de révolution d’axe de révolution (D) si :br les sections de (S) par des plans perpendiculaires à (D) sont des cercles de centre situé sur (D).

Vocabulaire :

Ces cercles sont appelés les parallèles à (S).

Exemple

1° Une sphère est une surface de révolution d’axe toute droite passant par son centre.
2° Ce cône est une surface de révolution d’axe de révolution, l’axe (Oz).

une parallèle de (S)

Génération d’une surface de révolution :

La rotation d’une courbe autour d’une droite fixe engendre une surface de révolution.

Cette courbe est appelée une génératrice.

Vocabulaire :

La section d’une surface de révolution par un demi-plan de frontière l’axe de révolution est appelée une méridienne.

Propriété

Toute méridienne est une génératrice de la surface de révolution.

La rotation de cette droite autour del'axe (Oz) engendre la surface de révolution, c'est une génératrice.

 

3 / Cylindre illimité : définition

soit un axe (Δ) et une droite (D) parallèle à (Δ).
La rotation de (D) autour de (Δ) engendre un cylindre illimité d’axe (Δ).
Si (D) est située à la distance r de (Δ) alors le cylindre est de rayon r.

Remarque

par définition, un cylindre illimité est une surface de révolution.

Propriété

toute droite passant par un point du cylindre et parallèle à (Δ) est une génératrice.

 

3/ Cylindre illimité : équation

Exemple d’équation de cylindre illimité :
Considérons le cylindre illimité (C) d’axe (Oz) et de rayon r.

Théorème

Le cylindre illimité (C) d’axe (Oz) et de rayon r est l’ensemble des points M ( x ; y ; z ) de l’espace
tels que:   x² + y² = r²

Démonstration

Soit M( x ; y ; z ) et soit H projeté orthogonal de M sur (Oz).
H a pour coordonnées ( 0 ; 0 ; z ).

 

3/ Cylindre illimité : section par un plan de référence

Considérons le cylindre illimité (C) d’axe (Oz) et de rayon r.
1° Section par un plan orthogonal à (Oz) :

Soit (P) d’équation z = a.
(P) ∩ (C) est le cercle de centre H ( 0 ; 0 ; a ) et de rayon r.


2° Section par un plan parallèle à (Oz) :
Soit par exemple le plan (P) d’équation y = a.

Il s’agit de l’intersection de deux plans non parallèles,par conséquent, c’est une droite.

Remarque

On obtiendrait les mêmes types d’intersection avec tout plan parallèle à l’axe (Oz),donc, en particulier,pour tout plan parallèle à (yOz).

 

4/ Cône illimité : définition

soit un axe ( Δ ) et une droite (D) sécante à (Δ).
La rotation de (D) autour de (Δ) engendre un cône illimité d’axe (Δ).
Le point A intersection de (D) et (Δ) est appelé sommet du cône.
L’angle géométrique formé par (D) et (Δ) est appelé angle du cône .
Cet angle est aussi appelé « demi-angle au sommet » du cône

Remarque

par définition, un cône illimité est une surface de révolution.

Propriété

toute droite passant par A et un point du cône est une génératrice.

 

4/ Cône illimité : équation

Exemple d’équation de cône illimité :

Considérons le cône illimité (C) d’axe (Oz), de sommet O et de demi-angle au sommet α.

Théorème :

Le cône illimité (C) d’axe (Oz) de sommet O et d’angle α
est l’ensemble des points M ( x ; y ; z ) de l’espace
tels que: x² + y² = z² tan² α

Démonstration

Soit M( x ; y ; z ) et soit H projeté orthogonal de M sur (Oz).
H a pour coordonnées ( 0 ; 0 ; z ).

Remarque

On tiendra le même raisonnement pour trouver l’équation de tout autre cône de sommet ou d’axe différents.

 

4/ Cône illimité : section par un plan de référence

Considérons le cône illimité (C) d'axe (Oz), de sommet O et de demi angle au sommet α

1° section par un plan orthogonal à (Oz)
Soit (P) d'équation z = a

(P) ∩ (C) est le cercle de centre h (0 ; 0 ; a) et de rayon |a tanα|

Remarque

Si a = 0 : ce cercle est réduit à un seul point : le sommet O
le plan passe alors par le sommet du cône 2° section parallèle à (Oz) :
Soit par exemple le plan (P) d'équation y = a



donc (P) ∩ (C) est constitué de deux droites :

- Si a ≠ 0 alors : il est possible de montrer que est une hyperbole.

On obtiendrai les mêmes types d'intersection avec tout plan parallèle à l'axe (Oz), donc, en particulier, pour tout plan parallèle à (yOz)