Cours maths Terminale S

Complexes - forme trigonométrique

Dans ce module, définition du module, de l’argument et de la forme trigonométrique d’un nombre complexe. Comme dans le module faisant le lien entre nombres complexes et géométrie plane, les définitions du module et de l’argument sont d’abord introduites en s’appuyant sur les vecteurs.

 

1/ Module d’un nombre complexe et norme.

Soit 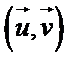base orthonormée du plan complexe.

Et soit un vecteur du plan d’affixe .

Par définition :

Le nombre réel est appélé module de est égale à .

Or si a pour coordonnées (x,y) d'après le théorème de pythagore

D'où pour tout élément de ℂ ,

Il est également à remarquer et à savoir que :

Donc : Deux nombres complexes sont égaux si et seulement si ils ont même module et même argument.

Ce qui se traduit du point de vue de la forme trigonométrique par :

Si les formes trigonométriques de z et z’ sont :


alors

 

2/ Exemples de calculs de modules

Ce qui est égale à ma valeur absolue de -5.
D'où ce choix de notation pour le module.



Ce qui est égal à valeur absolue de -3.

 

3/ Propriétés algébriques du module d'un nombre complexe

Si un nombre complexe est nul son module est nul.


Reciproquement :
Si le module d'un nombre complexe est nul alors ce nombre complexe est nul.
En effet :


Or la somme de deux carrés est nulle si et seulement si les deux carrés sont nuls.
D'où : x = 0 et y = 0
Donc : z = 0




Quelque soit z et z' élement de ℂ :
Le module du produit est égal au produit des modules.

Prémière conséquence, pour tout entier naturel n :

Autre conséquence : pour tout z élément de ℂ , avec z≠0 :
Le module du rapport est égal au rapport des modules.

Pour tout z et z' élément de ℂ, avec z' ≠ 0

Le module du rapport est égal au rapport des modules.

La demonstration de chacune de ces propriétés pourra faire l'objet d'un R.O.C

Attention !
De même que la norme de la somme ne vaut pas la somme des normes, le module de la somme ne vaut pas la somme des modules.

 

4/ Module d'un réel, module d'un imaginaire pur

D'où
Au sens de valeur absolue de x.
Donc si z réel : module de z = valeur absolue de z.
Sur IR moule et valeur absolue sont deux notions qui se confondent.

Remarque

z imaginaire pur avec y réel.

D'où
Ou tout simplement Donc |z| = |y| au sens de "valeur absolue de y".

 

5/ Module d'un nombre complexe et distance

Dans le plan complexe rapporté à un repère orthonormé, quels que soient les points A et B :

Dans la pratique, c'est surtout l'égalité : qui sert, mais pour être vraiment à l'aise en géométrie complexe, il faut maîtriser la quadruple égalité du dessus.

 

6/ Module d'un nombre complexe et point image

Soit z = x + yi élément de ℂ et M d'affixe z.
Par définition, les coorodnnées du point M dans le repère 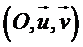sont les coordonnées du vecteur dans la base .
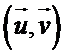et M ayant les mêmes coordonnées, ils ont donc la même affixe.

D'où
Par conséquent

Conclusion

Dans le plan complexe rapporté à un repère orthonormé : .
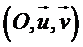Si z a pour image M alors |z| = OM.

Soit tout simplement

On peut aussi redemontrer cette formule en utlisant en prenant A = O et B = M.

Propriété

Les points situés sur le cercle trigonométrique ont une affixe dont le module vaut 1.

 

7/ Argument d’un nombre complexe et vecteur

Soit P le plan complexe muni d'une base 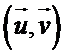et orienté dans le sens trigonométrique. Et soit un vecteur du plan non nul d'affixe .

Par définition :

Le nombre réel 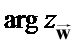noté et appelé argument de est égal à l'angle orienté .

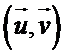Remarque:

1) Tout angle étant défini à 2π près.L'argument d'un complexe est donc lui aussi défini à un multiple de 2π près.

Autrement dit: Pour tout

2) On ne peut former un angle orienté avec le vecteur nul, c'est pour cette raison que ce vecteur est exlu de la définition.

 

8/ Argument d'un nombre complexe et point d'image

Soit P le plan complexe muni d'un repère orthonormé 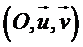et orienté dans le sens trigonométrique.

Soit z = x + yi non nul élément de ℂ et M d'affixe z.

Par conséquent :

Conclusion

Dans le plan complexe muni d'un repère orthonormé 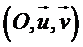et orienté dans le sens trigonométrique.

Si z ≠ 0 a pour image M alors :

Soit tout simplement pour M ≠ 0

 

9/ Exemples d’arguments

Soit P le plan complexe muni d'un repère orthonormé 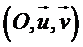et orienté dans le sens trigonométrique.

 

10/ Caractérisation des réels et des imaginaires purs à l’aide de l’argument

Soit P le plan complexe muni d'un repère orthonormé 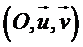et orienté dans le sens trigonométrique.








z imaginaire pur à partie imaginaire > 0


z imaginaire pur à partie imaginaire

 

11/ Coordonnées cartésiennes, coordonnées polaires

Soit P le plan complexe muni d'un repère orthonormé 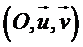et orienté dans le sens trigonométrique.

Soit M un point du plan different de O.

Il existe deux façons de rpérer la position de M dans ce repère :
- Par ses coordonnées, cartésiennes : (x , y).
- Et par ses coordonnées polaires (r, θ) .

Avec

Or M ayant pour affixe z = x + yi

Conclusion

Le couple ( |z| , argz) représente les coordonnées polaires de M(z).

Grâce aux nombres complexes on va donc pouvoir travailler à la fois en coordonnées polaires et coordonnées cartésiennes. En utilisant les formules de trigonométrie dans le triangle rectangle colorié, on obtient :

 

12/ Forme trigonométrique : existence

Donc pour tout z non nul, tel que : z = x + yi
On a :
Soit :
Que l'on préférera écrire pour des questions de lisibilité : z = r (cosθ + sinθi)

Conclusion

Dans le plan complexe muni d'un repère orthonormé : 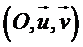et orienté dans le sens trigonométrique.

Tout nombre complexe non nul peut s'écrire peut s'écrire : z = r (cosθ + sinθi)

Où :

En effet, pour que cette écriture puisse représenter tous les complexes non nuls il faut que θ balaye un intervalle semi-ouvert de longueur 2π .

On choisit l'intervalle ]-π,π] , intervalle contenant toutes les mesures principales des angles.
Cette écriture est appelée forme trigonométrique du complexe.

Cependant attention toute écriture qui à l’air trigonométrique n’en est pas forcément une !

Par exemple :

n'est pas écris sous forme trigonométrique car : -5

Remarque :

Nous verrons dans la partie exercice comment trouver la bonne écriture trigonométrique de ce nombre.

 

13/ Forme trigonométrique : unicité

Plus généralement, soit l'écriture trigonométrique de z obtenue à l'aide de son module et de son argument :

Et soit une autre écriture de z du type : .

Remarque et propriété :

Pour tout réel

Donc :
D'où :
Pour que : soit l'écriture trigonométrique de z, il faut donc pour commencer : r' > 0
Or si r' > 0 : alors r' = r

D'où :

Conclusion

L'écriture trigonométrique d'un nombre complexe est unique.

Raison pour laquelle 0 ne peut avoir d'écriture trigonométrique car en prenant r = 0, une infinité de valeur en prenant θ serait possible, et l'écriture de 0 ne serait donc pas unique.

D'un point de vue pratique : est l'écriture trigonométrique de z
si et seulement si r' > 0

Auquel cas :
Une stratégie pour mettre un nombre sous forme trigonométrique pourra donc parfois consister à calculer le module, à le mettre en facteur, puis à réussir à mettre le facteur restant sous la forme
cosθ + i sinθ

 

13/ Forme trigonométrique : égalité

Deux points du plan complexe sont confondus
si et seulement si
ils ont les mêmes coordonnées polaires.

Donc : deux nombres complexes sont égaux
si et seulement si
ils ont même module et même argument.

ce qui se traduit du point de vue de la forme trigonométrique par :
Si les formes trigonométrique de z et z' sont :

Alors :

 

14/ Passage de la forme algèbrique à la forme trigonométrique

Exemple :

Soit
L'objectif est de l'écrire sous la forme trigonométrique :


Il faut commencer par calculer le module de z.


Maintenant, on met le module en acteur dans z.



C'est alors qu'il faut être capable de reconnaitre l'angle à partir de son cosinus et de son sinus. Il faut donc bien maîtriser les angles de référence.

Remarque concernant le tracé de M(z) :

Soit
Sous cette forme algébrique, il est difficile de tracer M d’affixe z avec précision.
Mais grâce à la forme trigonométrique : cela devient possible.

En effet, le module vaut 4 donc M est sur le cercle de centre O et de rayon 4.
Pour trouver ensuite sa position sur le cercle, on peut le faire de trois façons :
- Soit à l’aide de l’ordonnée de M.

Les coordonnées de M étant positives,Il ne peut être que dans ce quart de plan.

Donc on ne trace qu’un quart de cercle.

- Soit en traçant à l’aide d’un triangle équilatéral.


- Soit en traçant à l’aide du cercle trigo.

 

15 / Propriétés algébriques de l’argument d’un nombre complexe

Remarque

Les propriétés à venir ne concernent que des nombres complexes non nuls et les égalités sont vraies à 2kπ près .

Du critère d'égalité de deux nombres complexes sous forme trigonométrique, du module du produit égal au produit des modules et des formules d'addition des sinus et cosinus découle la propriété suivante :

Quels que soient z et z’ éléments de ℂ^* :
L'argument du produit est égal à la somme des arguments.

Première conséquence, pour tout entier naturel n et z non nul :

Autre conséquence : pour tout z élément de ℂ: z ≠ 0

et enfin, conséquence de et

Pour tout z et z’ éléments de ℂ^* :
L'argument du rapport est égal à la différence des arguments.



La démonstration de chacune de ces propriétés pourra faire l’objet d’un R.O.C.

 

16 / Configuration de reference

M'' étant le symétrique de M par rapport à O, on a donc d'après les propriétés de la symétrique centrale :

 

17 / Bilan

Dans le plan complexe muni d'un repère orthonormé 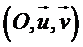: et orienté dans le sens trigonométrique, tout problème de géométrie plane peut donc se ramener à un " simple " calcul sur les complexes.

A condition de bien savoir utiliser les correspondances suivantes :