Cours maths Terminale S

Complexes - forme exponentielle

Dans ce module, définition, manipulation et étude de l’écriture d’un nombre complexe sous forme exponentielle.
Dans un premier temps le cours est consacré à l’étude des nombres complexes de module 1.

 

1/ Nombre complexe de module 1

Dans le plan complexe rapporté à un repère orthonormé :
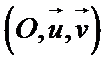
Tout nombre complexe non nul peut s'écrire sous forme trigonométrique :

Réciproquement :

Or : 1>0 donc par unicité de l’écriture trigonométrique :

D’où l’équivalence :

1/ Nombre complexe de module 1

Résultat évident d’un point de vue géométrique car :

A chaque point du cercle correspond une valeur de θ.
θ balaye donc un intervalle semi-ouvert de longueur 2π.

Si l’intervalle sur lequel est pris θ est d’une longueur inférieure à 2π alors M ne décrit qu’un arc de cercle.

 

2/ Notation exponentielle

Pour des raisons d'analogie avec la fonction exponenetielle, que nous verrons plus loin, on décide de noter :

Se lit " exponentielle de i θ" ou encore plus simplement : " é - i - téta " .

D’où une équivalence globale :

Il faut savoir lire et utiliser ces multiples équivalences dans tous les sens et avoir compris en particulier que :

e^iθ est le nombre complexe de module 1 et d’argument θ.

ou encore que :

Tout nombre complexe de module 1 peut s’écrire e^iθ , θ étant son argument.

 

3/ Quelques valeurs de référence

e^iθ est le nombre complexe de module 1 et d'argument θ

Donc, en particulier : e^iθ est le nombre complexe de module 1 et d’argument 0.

D'où : D'où    e^iθ = 1

Par un même raisonnement graphique, on obtient :

e^iπ = - 1

mais on notera plutôt avec le signe "-" devant

D'où

Resultat que l'on peut aussi retrouver par le calcul :

 

4/ Notation exponentielle du conjugué et de l'opposé

Nous pouvons nous aider de la configuration

 

5/ Propriétés algébriques de la notation exponentielle

Produit de deux exponentielles: e^iθ x e^iθ'

e^iθ x e^iθ' est le nombre complexe de module 1 et d'argument θ + θ' donc :

Cette égalité ainsi que celle-ci : e^iθ = 1
sont les deux « équations fonctionnelles » que doit vérifier une fonction pour être une fonction exponentielle.

La notation e^iθ se justifie donc.

Remarque :

On peut retrouver le resultat démontré géometriquement sur (e^-iθ)

Puissance d'une exponentielle :

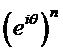
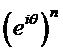est le nombre complexe de module 1 et d'argument nθ donc :

On peut également le déduire comme première conséquence du resultat ci-dessus en utilisant une demonstration par recurrrence.

Deuxième conséquence de la propriété sur le produit :

Inverse d'une exponentielle :

donc :

On peut également le démontrer en utilisant module et argument comme vu plus haut.

Remarque :

1) On peut retrouver le résultat démontré géométriquement
donc :

2) On peut diviser par e^iθ car son module vaut 1 il ne peut être nul.

Conséquence des propriétés sur le produit et l'inverse :

Quotient de deux exponentielles :

La propriété N°2 peut aussi être écrite ainsi :
sous cette forme, elle est appellée Formule de Moivre

En résumé, la notation exponentielle a les mêmes propriétés que la notation puissance.

Ces propriétés sont donc très simples à retenir et leur manipulation est très intuitive.
Leur démonstration pourra faire l’objet d’un R.O.C.

 

6/ Forme exponentielle : existence

Rappel sur la forme trigonométrique :

Dans le plan complexe muni d’un repère orthonormé : 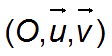et orienté dans le sens trigonométrique.

Tout nombre complexe non nul peut s’écrire :

cette écriture est appelée : forme exponentielle du nombre complexe.

Cependant, attention toute écriture qui à l’air exponentielle n’en est pas forcément une !

Par exemple :

n'est pas écrit sous forme exponentielle car -5

Remarque :

Nous verrons dans la partie exercice comment trouver la bonne écriture exponentielle de ce nombre

 

7/ Forme exponentielle : unicité

Rappel :

L'écriture trigonométrique d'un nombre complexe non nul est unique.

Et d'un point de vue pratique :
est l'écriture trigonométrique de z si et seulement si r' > 0
auquel cas

Donc :
L'écriture exponentielle d'un nombre complexe est unique.
et d'un point de vue pratique :
est l'écriture exponenetielle de z si et seulement si r' > 0
auquel cas

Une stratégie pour mettre un nombre sous forme exponentielle pourra donc parfois consister à calculer le module, à le mettre en facteur,puis à réussir à mettre le facteur restant sous la forme : e^iθ

 

7/ Forme exponentielle : égalité

Rappel :

Si les formes trigonométriques de z et z' sont :


alors :

donc : si les formes exponentielles de z et z' sont :

alors :

En particulier pour r = r' = 1.

 

7/ Forme exponentielle : résumé

Nous pouvons donc étendre notre équivalence de départ à tout nombre complexe non nul.

Remarque

Pour passer de la forme algébrique à la forme exponentielle ou inversement,il faut passer par la forme intermédiaire qu’est la forme trigonométrique.

7/ Forme exponentielle :conjugué et opposé

7/ Forme exponentielle : calculs

Du fait de ses propriétés semblables à celles d’une puissance,la notation exponentielle est idéale pour pratiquer des calculs sur les complexes.
En particulier quand ces calculs sont des produits, des puissances ou des quotients.

Exemples :

1° Montrer que est un réel.

On aurait également pû faire ce calcul à l'aie de deux carrés ou de la formule du binôme de Newton.

Tout d'abord, mettons 3 + 3i sous forme exponentielle.

2° Montrer que est imaginaire pur.

On pourrait tout à fait mener ce calcul de façon algébrique mais nous allons choisir la stratégie exponentielle.

Toute cette étape pouvant être faite de tête ou au brouillon

 

 

8/ Formules d’Euler

Remarque

Comme

On peut par exemple redémontrer ce résultat de la sorte :

 

9/ Equation paramétrique d’un cercle : démonstration

Soit C le cercle de centre Ω et de rayon R .

Or 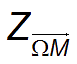admet une écriture exponentielle qui est :

De plus quand M parcourt C , 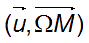décrit l’intervalle ] - π ; π]

Illustration

Ce résultat est très simple à retrouver et à expliquer graphiquement :

En effet, tout cercle de rayon R est le translaté d'un cercle de centre O et de même rayon.

En résumé :

Ω qui représente l’angle 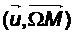est le paramètre : à chaque valeur de θ prise dans un intervalle de longueur 2π correspond un unique point du cercle, et inversement.