Cours maths 5ème

Le carré

Après avoir défini ce qu’est un carré, des activités guidées permettront de découvrir qu’un carré est à la fois un losange et un rectangle et qu’il a les propriétés de ces deux figures. Il sera ensuite rappelé comment montrer qu’un quadrilatère est un carré à partir de ses côtés et de ses angles, de ses particularités ou de ses diagonales.

 

Définition du carré

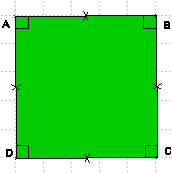Le quadrilatère ABCD a 4 côtés de la même longueur et 4 angles droits:

C’est un carré.

Définition :

Un carré est un quadrilatère qui a ses quatre côtés de la même longueur et ses quatre angles droits.

Un quadrilatère particulier

Par définition :

Le carré a quatre côtés de la même longueur ...

Propriété 1 :
Le carré, puisqu’il a 4 côtés de la même longueur, est un losange. Il a donc toutes les propriétés du losange.

 

Les propriétés du carré liées au losange

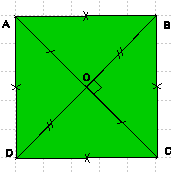Le carré ABCD est un losange, donc :
* Les côtés opposés du carré sont parallèles.
* Ses diagonales se coupent en leur milieu et sont perpendiculaires.
* Ses diagonales sont des axes de symétrie.
* Le point d’intersection des diagonales est le centre de symétrie.

Un quadrilatère particulier

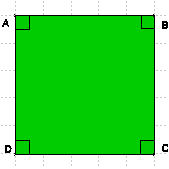Par définition :

Le carré a quatre angles droits ...

Propriété 2 :
Le carré, puisqu’il a 4 angles droits, est un rectangle. Il a donc toutes les propriétés du rectangle.

 

Les propriétés du carré liées au rectangle

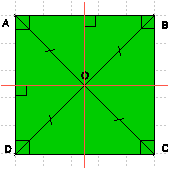Le carré ABCD est un rectangle, donc :
* Les côtés consécutifs du carré sont perpendiculaires.
* Ses diagonales se coupent en leur milieu et sont de même longueur.
* Ses médiatrices sont des axes de symétrie.
* Le point d’intersection des diagonales est le centre de symétrie.

 

Les diagonales du carré

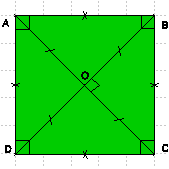Propriété 3 :
Les diagonales du carré se coupent en leur milieu, sont perpendiculaires et ont la même longueur.

 

Les éléments de symétrie du carré

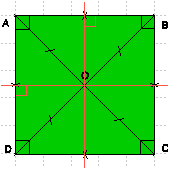Propriété 4 :
Un carré a quatre axes de symétrie : ses diagonales et les médiatrices de ses côtés.

Un carré a un centre de symétrie : le point d’intersection de ses diagonales.

 

Reconnaître un carré

Le quadrilatère ABCD a 4 côtés de même longueur et 4 angles droits.

ABCD est donc un carré

Propriété 5 :
Si un quadrilatère a 4 côtés de même longueur et 4 angles droits, alors ce quadrilatère est un carré.

Un rectangle particulier

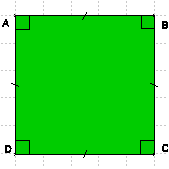ABCD est un rectangle.
Ses côtés opposés ont la même longueur, ainsi :
AB = DC et BC = AD
En supposant que AB = BC.
Alors : AB = BC = CD = DA

Le rectangle ABCD a donc 4 côtés de même longueur, c’est aussi un losange. ABCD est donc un carré.

Un losange particulier

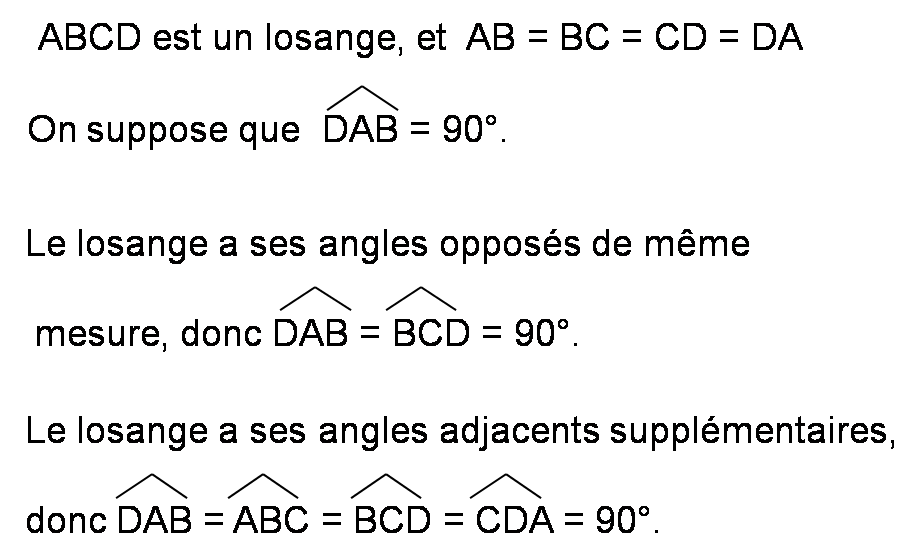
Le losange ABCD a donc 4 angles droits ; c’est aussi un rectangle.
ABCD est donc un carré.

 

Reconnaître un carré

Propriété 6 :
Si un quadrilatère est à la fois un rectangle et un losange, alors ce quadrilatère est un carré.

 

Reconnaître un carré par ses diagonales

Propriété 7 :
Si un quadrilatère a ses diagonales qui ont le même milieu , qui sont perpendiculaires et qui ont la même longueur, alors c’est un carré

Propriété 8 :
Si un parallélogramme a ses diagonales qui sont perpendiculaires et qui ont la même longueur, alors c’est un carré.

Propriété 9 :
Si un losange a ses diagonales qui ont la même longueur, alors c’est un carré.

Propriété 10 :
Si un rectangle a ses diagonales qui sont perpendiculaires, alors c’est un carré.