Cours maths Terminale S

Barycentre

Le cours de ce module est un rappel des définitions et propriétés du barycentre dans le but de les appliquer à la résolution de problèmes liés à l’espace.

 

1/ Défintion du barycentre

Définition

Soit le système de points pondérés de l’espace : { ( A ; a ) ; (B ; b ) ; ( C ;c ) }.
Si la somme des coefficients a+b+c est non nulle alors :
il existe un unique point G de l’espace tel que :
Ce point est appelé barycentre des points A, B et C affectés des coefficients a, b et c
Et noté : G bar ( A ; a ) ( B ; b ) ( C ; c ).

Remarques

1) Les coefficients sont définis à un multiple près, c’est à dire que, pour tout réel k :
G bar ( A ; ka ) ( B ; kb ) ( C ; kc ) = G bar ( A ; a ) ( B ; b ) ( C ; c ).

2) Si a = b = c alors G est appelé isobarycentre des points A, B et C.
Pour 2 points A et B, l’isobarycentre de A et B est leur milieu.
Pour trois points A, B et C, l’isobarycentre est le centre de gravité du triangle ABC.

3) Le barycentre existe si et seulement si la somme des coefficients est non nulle.

 

2/ Propriétés du barycentre

Propriété fondamentale:

soit G bar ( A ; a ) ( B ; b ) ( C ; c )
Pour tout point M de l’espace :

Conséquences :

1° Position du barycentre :

* Soit G bar ( A ; a ) ( B ; b).
Pour tout point M de l’espace :
Donc, en particulier en prenant M = A :
Le point G appartient donc à la droite (AB).
D’où la propriété :
►Si G bar ( A ; a ) ( B ; b) alors A, B et G sont alignés.

Réciproquement : tout point de la droite (AB) peut s’écrire comme barycentre de A et de B.

* Soit G bar ( A ; a ) ( B ; b) ( C ; c ).
Pour tout point M de l’espace :
Donc, en particulier en prenant M = A :

Les vecteurs sont coplanaires donc G appartient au plan (ABC).
D’où la propriété : ►Si G bar ( A ; a ) ( B ; b) ( C ; c ) alors G appartient au plan (ABC).

Réciproquement : tout point du plan (ABC) peut s’écrire comme le barycentre de A, B et C.

2° Coordonnées du barycentre :

Considérons l’espace rapporté au repère orthonormé :

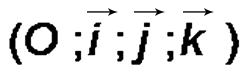
Soit G bar ( A ; a ) ( B ; b) ( C ; c ).

Pour tout point M de l’espace :

Donc, en particulier en prenant M = O :

L’abscisse du barycentre est la moyenne pondérée des abscisses.

L’ordonnée du barycentre est la moyenne pondérée des ordonnées.

La côte du barycentre est la moyenne pondérée des côtes

3° Propriété d’associativité du barycentre :

Soit G bar ( A ; a ) ( B ; b) ( C ; c ) et soit I bar ( B ; b ) ( C ; c ).
Alors : G bar ( A ; a ) ( I ; b+c ).

Démonstration

G bar ( A ; a ) ( B ; b) ( C ; c ) donc :

I bar ( B ; b ) ( C ; c ) donc pour tout point M de l’espace :

Donc en particulier pour M = G :

Par conséquent :
a+b+c ≠ 0 donc G bar ( A ; a ) ( I ; b+c )

Remarque

Cette propriété est très utilisée pour montrer l’appartenance d’un point à une droite.
Elle sert, en particulier, à démontrer que l’isobarycentre de 3 points est leur centre de gravité.

 

3/ Réduction de sommes vectorielles

Dans les exercices de recherche d’ensembles de points, on est souvent confronté au besoin de réduire des sommes vectorielles du type :

Deux cas sont possibles :

Cas n° 1 : la somme des coefficients est non nulle.
Alors, le barycentre du système { ( A ; a ) ; ( B ; b ) ; ( C ; c ) } existe,


Cas n° 2 : la somme des coefficients est nulle.
Alors, le barycentre du système { ( A ; a ) ; ( B ; b ) ; ( C ; c ) } n’existe pas, et il faut utiliser la relation de Chasles pour éliminer le point M :


La somme est alors indépendante de M et égale au vecteur constant :

Exemple n° 1

Dans l’espace rapporté au repère orthonormé :
On considère les points A ( 1 ; 2 ; -1 ), B ( 0 ; 2 ; 1 ) et C ( 3 ; -2 ; 2 ).

Déterminer la nature et les éléments caractéristiques de l’ensemble (E) des points M de l’espace tels que :

1 + 2 −1 = 2 ≠ 0 donc le système { ( A ; 1 ) ; ( B ; 2 ) ; ( C ; -1 ) } admet un barycentre.
Appelons-le G. On a alors d’après la propriété fondamentale du barycentre :
pour tout point M de l’espace :

1 + 1 − 2 = 0 donc le système { ( A ; 1 ) ; ( B ; 1 ) ; ( C ; -2 ) } n’admet pas de barycentre.
En utilisant la relation de Chasles :
D'où :


(E) est donc la sphère de centre G et de rayon

Exemple n° 2

Dans l’espace rapporté au repère orthonormé :
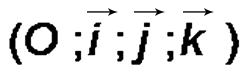
On considère les points A ( 1 ; 2 ; -1 ), B ( 0 ; 2 ; 1 ) et C ( 3 ; -2 ; 2 ).
Déterminer la nature et les éléments caractéristiques de l’ensemble ( E ) des points M de l’espace tels que :

Avec G bar ( A ; 1 ) ( B ; 2 ) ( C ; -1 ), pour tout point M de l’espace :

Soit I le milieu du segment [AB].
I est l’isobarycentre de A et de B et on a alors pour tout point M de l’espace :



(E) est l’ensemble des points équidistants de G et de I.
(E) est donc le plan médiateur du segment [GI].

Exemple n° 3

Dans l’espace rapporté au repère orthonormé :
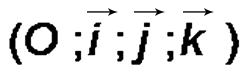
On considère les points A ( 1 ; 2 ; -1 ), B ( 0 ; 2 ; 1 ) et C ( 3 ; -2 ; 2 ).

Déterminer la nature et les éléments caractéristiques de l’ensemble ( E ) des points M de l’espace tels que :

Avec G bar ( A ; 1 ) ( B ; 2 ) ( C ; -1 ), pour tout point M de l’espace :



(E) est le plan orthogonal à (AB) passant par G.