Cours de maths à partir de 9.90 €/heure
Cours maths Terminale S
Equations de plans
Ce module traite les différentes façons de définir un plan de l’espace : définition à partir de 3 points non alignés, définition à partir d’un point et de deux vecteurs non colinéaires et définition à partir d’un point et d’un vecteur normal.
1/ Définition(s) d’un plan de l’espace
Par deux points distincts A et B passe une unique droite, appelée la droite (AB).
Par ces deux points passent une infinité de plans, qui ont en commun la droite (AB).
On peut imaginer ces plans, pivotant autour de la droite (AB).
Pour fixer le plan pivotant autour de (AB), il faut choisir un point C extérieur à (AB)..
Définition n° 1 d’un plan :
Il existe un unique plan passant par 3 points non alignés A, B et C.
D’un point de vue pratique :
3 points de l’espace définissent un plan si et seulement si ces 3 points ne sont pas alignés.
Pour prouver que les points A, B et C ne sont pas alignés, il suffit de montrer, par exemple, que les vecteurs et
ne sont pas colinéaires.
Une droite du plan peut être définie par la donnée de deux points distincts ou par la donnée d’un point et d’une direction.
De même, un plan de l’espace peut être défini par la donnée de 3 points non alignés ou par la donnée d’un point et d’une direction.
Cette direction peut notamment être définie par la donnée de deux vecteurs non colinéaires.
Définition n°2 d’un plan :
Un plan est entièrement défini par la donnée d’un point A de l’espace et de deux vecteurs non colinéaires.
On dit que .png) est un couple de vecteurs directeurs du plan (P).
est un couple de vecteurs directeurs du plan (P).
Alors, pour tout point M de (P), il existe un couple unique de réels ( k ; k ‘) tel que :
Réciproquement :
S'il existe un couple de réels ( k ; k' ) tels que : alors M
au plan (P).
On a donc : M (P) si et seulement si il existe un couple ( k , k' ) tel que
Si l'espace est muni d'un repère orthonormé et
si et alors :
Ce système est appélé représentation paramétrique du plan.
passant par le point et de vecteurs directeurs :
A tout point M de (P) correspond un unique couple de paramètres ( k ; k’ ) et inversement.
Remarque :
Les vecteurs ,
.png) et
et sont dits coplanaires. C’est à dire qu’il est possible
de trouver 3 représentants de ces vecteurs situés dans un même plan.
On a ici :
Plus généralement :
Théorème :
Les vecteurs ,
.png) et
et sont coplanaires si et seul7ement si l’un des vecteurs peut s’écrire
comme une combinaison linéaire des deux autres.
Par exemple, s’il existe un couple de réels ( k ; k’ ) tel que : alors ces 3 vecteurs sont coplanaires.
Théorème :
Si deux plans sont orthogonaux à une même droite alors ces plans sont parallèles entre eux.
Une direction de plan peut donc être définie par orthogonalité à une droite donnée,ou encore par orthogonalité à un vecteur donné.
En terme de vecteur, on ne parle alors plus de vecteur directeur mais de
vecteur normal.
Définition n°3 d’un plan :
Un plan est entièrement défini par la donnée d’un point A de l’espace et d’un vecteur normal.
Ou encore, il existe un unique plan passant par un point donné et orthogonal à une droite donnée.
2/ Équation cartésienne d’un plan
Soit le plan (P) passant par le point A et de vecteur normal .
On a alors :
D’où, si l’espace est rapporté à un repère orthonormé
et si .png) et
et alors :
Théorème :
Si est un vecteur normal au plan (P) alors (P) a une équation cartésienne du type :
Cette équation est appelée
équation cartésienne du plan (P).
Théorème :
Si est un vecteur normal au plan (P) alors (P) a une équation cartésienne du type :
Reciproque :
SI (P) a une équation cartésienne du type : alors le vecteur
est un vecteur normal au plan (P).
Exemple de recherche de l’équation cartésienne d’un plan:
Soit le plan (P) passant par A ( 1 ; 2 ; -3 ) et de vecteur normal
(P) a une équation cartésienne du type : .
Et A ( 1 ; 2 ; -3 ) (P) donc :
D’où l’équation cartésienne de (P) :
On peut également utiliser le produit scalaire, comme vu à la diapositive précédente :
3/ Notion de demi-espace
Théorème :
Soit (P) plan de l’espace d’équation cartésienne :
et soit A un point de l’espace tel que : .
Alors, l’ensemble des points M ( x ; y ; z ) de l’espace tels que : est le demi-espace ouvert de frontière (P) contenant A.
De même, l’ensemble des points M ( x ; y ; z ) de l’espace tels que : est le demi-espace ouvert de frontière (P) ne contenant pas A.
Exemple :
e plan (ABC) a pour équation cartésienne :
Donc, l’ensemble des points M (x ; y ; z ) tels que : est le demi-espace ouvert de frontière (ABC) contenant O.
4/ Position relative de deux plans
De même que dans le plan, deux droites sont parallèles ou sécantes, dans l’espace, deux plans sont parallèles ou sécants.
Deux plans sont parallèles s’ils ont la même direction.
Or, comme nous l’avons vu, une direction de plan peut être donnée par un vecteur normal.
Théorème
Deux plans sont parallèles si et seulement si ils possèdent deux vecteurs normaux colinéaires.
Exemple
Soit (P) d’équation cartésienne :
Et soit (Q) d’équation cartésienne :
(P) a pour vecteur normal :
Et (Q) a pour vecteur normal :
donc (P) et (Q) sont parallèles.
Attention !
Une équation cartésienne est toujours définie à un multiple près.
Pour savoir si ces deux plans sont parallèles
confondus, il faut simplifier les deux équations, de sorte à avoir les 3 premiers coefficients identiques :s
On ne touche pas à l’équation de (P) :
On divise par (-2) l’équation de (Q) :
Les deux derniers coefficients sont différents, il s’agit donc de deux équations différentes.
Les plans (P) et (Q) sont donc
strictement parallèles.
On peut également le justifier de la façon suivante :
Par exemple : le point A ( 0 ;-5 ;0 ) appartient à (P).
Or : donc A n’appartient pas à (Q).
Les plans ne peuvent donc être confondus.
Théorème
Deux plans non parallèles sont sécants et leur intersection est une droite.deux plans parallèles
Remarque
L’étude détaillée de l’intersection de deux plans sera faite dans le prochain module. Nous apprendrons entre autre à passer du système des deux équations cartésiennes,définissant l’intersection des plans, au système de représentation
paramétrique de la droite.
Cas particulier :
deux plans sécants peuvent être orthogonaux.
Ces plans n’étant pas parallèles, ils sont sécants.
On peut donc également les qualifier de
plans perpendiculaires.
Théorème
Deux plans sont perpendiculaires si et seulement si leurs vecteurs normaux sont orthogonaux.
En pratique, il suffira donc de montrer que :
5/ Position relative d’une droite et d’un plan
Soient (d) une droite de l’espace et (P) un plan de l’espace.
(d) peut se positionner de différentes façons par rapport à (P) :
Cas n° 1 : (d) est parallèle à (P).
C’est le cas si (d) est parallèle à une droite (d’) de (P).
Tout vecteur directeur de (d) est alors un vecteur directeur de (P) et se trouve donc orthogonal au vecteur normal de (P).
Pour montrer (d) // (P), il suffit donc de montrer
qu’un vecteur directeur de (d) est orthogonal à un vecteur normal
de (P).
Deux cas de parallélisme sont possibles :
1° (d) est
strictement parallèle à (P), auquel cas : Ø.
2° (d) est
incluse dans (P), auquel cas : (d)
En montrant, par exemple, que leur produit scalaire est nul.
Réciproquement :Si (d) // (P) alors :
tout vecteur normal à (P) est orthogonal
à tout vecteur directeur de (d).
deux cas de parallélisme sont possibles :
1) (d) est strictement parallèle à (P), auquel cas : Ø.
2) (d) est incluse dans (P), auquel cas : (d).
Remarque pratique :
Il existe plusieurs façons de montrer qu’une droite (d) est incluse dans un plan (P).
Une première méthode consiste à montrer dans un premier temps que (d) est parallèle à (P) puis dans un deuxième temps qu’un point de (d) appartient à (P).
Une deuxième méthode consiste à montrer directement que tout point de (d) appartient à (P).
Pour ce faire, on utilise une représentation paramétrique de (d), ce que nous verrons dans le prochain module.
Cas n° 2 : (d) est sécante à (P).
position relative d'un plan C’est le cas si (d) n’est pas parallèle à (P).
Attention !
Si (d) est incluse dans (P), on ne dira donc pas que (d) est sécante à (P).
(d) est sécante à (P) si et seulement si l’intersection de (d) et de (P) est un point.
Pour montrer (d) est sécante à (P), il suffit de montrer que (d) n’est pas parallèle à (P).
Autrement dit que vecteur directeur de (d) n'est pas orthogonal à vecteur normal
de (P).
Cas particulier : (d) est orthogonale à (P).
La définition géométrique de l’orthogonalité d’une droite par rapport à un plan a été vue dans le module traitant du produit scalaire et de l’orthogonalité.
Limitons nous donc ici à l’aspect pratique, à savoir :
Pour montrer qu’une droite (d) est orthogonale à un plan (P), il suffit de montrer qu’un vecteur directeur de (d) est colinéaire à un vecteur normal
de (P).
Et réciproquement : Si (d) est orthogonale à (P) alors :
tout vecteur directeur de (d) est colinéaire à un vecteur normal de (P).
Ceci reposant sur le fait que :
Si deux droites sont parallèles, tout plan orthogonal à l’une est orthogonal à l’autre.
6/ Distance d’un point à un plan
Définition
Soit un plan (P) et soit un point A.
On appelle distance du point A au plan (P) la plus petite distance entre un point M du plan (P) et le point A.
On la note : d ( A ; (P)).
Théorème :
d ( A ; ( P ) ) = AH où H est le projété orthogonal de A sur ( P ).
En effet, d’après le théorème de Pythagore, pour tout M de (D) :
.png)
Théorème :
Dans l'espace muni d'un repère orthonormé : la distance du point A au plan ( P ) d'équation cartésienne : ax + by + cz + d = 0 est :
- en nominateur : Valeur absolue de « l’équation de (P) » appliquée au point A.
- en dénominateur : Norme du vecteur normal de coordonnées ( a ; b ; c ).
Remarque
si A appartient à (P), on retrouve bien d(A; (P))=0.
7/ Position relative d’une sphère et d’un plan
Soit un plan (P) et une sphère (S) de centre et de rayon R.
(S) peut se positionner de différentes façons par rapport à (P).
Cas n° 1 : (S) ne coupe pas (P).
C’est le cas si la distance de à (P) est strictement supérieure à R.
On a donc :
Cas n° 2 : (S) est tangente à (P).
L’intersection entre (S) et (P) se réduit alors à un point unique.
Ce point étant le projeté orthogonal H de sur (P).
C’est le cas si la distance de (P) est égale à R.
On a donc :
Cas n° 2 : (S) est tangente à (P).
L’intersection entre (S) et (P) se réduit alors à un point unique.
Ce point étant le projeté orthogonal H de sur (P).
C’est le cas si la distance de (P) est égale à R.
On a donc :
Cas n° 3 : (S) coupe (P) selon un cercle.
C’est le cas si la distance de à (P)
est strictement inférieure à R.
On a donc :
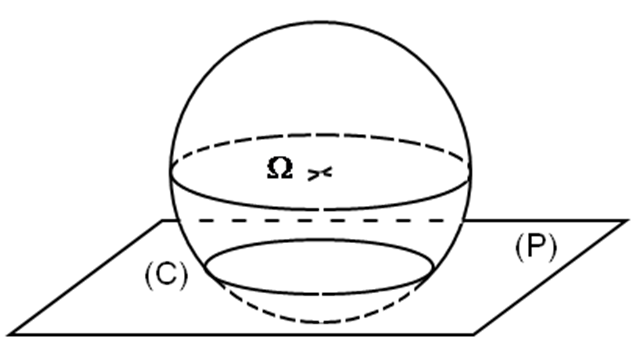
Le cercle d’intersection (C) a alors pour centre H, projeté orthogonal de sur (P).
Pour trouver son rayon, il suffit d’utiliser le théorème de Pythagore :
étant égale à la distance de à (P)
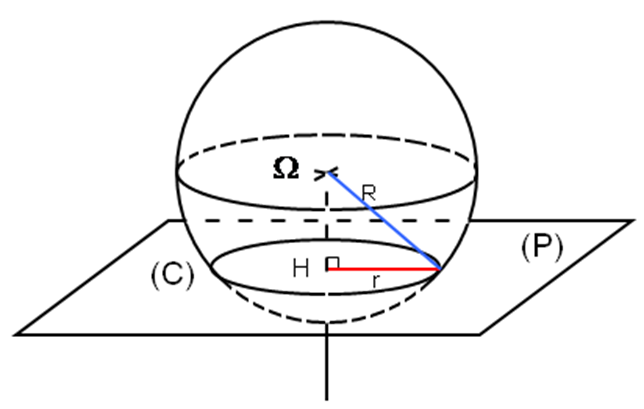
Remarque
1) Ce dernier résultat n’est pas à apprendre mais à savoir retrouver.
2) Dans le cas où (S) est tangente à (P), on peut estimer que l’intersection
est le cercle de centre H et de rayon 0.
3) Si
appartient à (P) alors (C) a pour rayon R, rayon de la sphère.
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.