Cours maths Terminale S
Complexes - équations
Dans ce module, étude de la résolution d’équations dans l’ensemble des complexes et de la représentation des nombres complexes dans le plan.
1/ Equations du premier degré dans ℂ
On résout les équations du premier degré dans ℂ de même que dans ℝ
Exemple
Résoudre l'équation 2iz + 3 = 4i + 5z
L’objectif étant de trouver la solution et de la mettre sous forme algébrique.
La stratégie ici, consiste à manipuler l’équation afin d’avoir z dans un seul membre et de pouvoir le mettre en facteur.
En enlevant 5z puis 3 aux deux membres de l’égalité, on obtient :
Attention !
Avant d'utiliser son conjugué, il faut mettre ce nombre (2i - 5) sous forme algébrique.
La solution de l'équation est donc
2/ Equations utilisant la forme algébrique
Pour résoudre certaines équations dans ℂ , il est parfois nécessaire de mettre l'inconnue sous forme algébrique, pour pouvoir utiliser l'une des propriétés suivantes :
Un nombre complexe est nul si et seulement si sa partie réelle et sa partie imaginaire sont nulles.
Ou sa conséquence :
Deux nombres complexes sont égaux
si et seulement si
ils ont même partie réelle et même partie imaginaire.
Exemple
Résoudre l'équation
posons
z = x + yi
Alors, z solution de
Il faut maintenant mettre ce membre sous forme algébrique. 
La solution de l’équation est donc:
3/ Equations du second degré dans ℂ
Rappel dans ℝ sur un exemple :
Soit l'équation
x2 − 2x -3 = 0
calcul du discriminant
donc
Δ
possède deux racines opposées réelles
par conséquent, l'équation admet : deux solutions réelles
Transposition à ℂ
Soit l'équation
z2 −2z +2 =0
calcul du discriminant
donc Δ possède deux racines opposées imaginaires pures :
par conséquent, l'équation admet : deux solutions complexes.
Il est à noter que ces deux racines complexes sont conjuguées.
Cas général et bilan
Soit l'équation
avec a, b et c élément de ℝ.
possède toujours
dans ℂ
deux racines opposées :
r1 et r2
et l' équation a pour solution(s) :
Qui ne peuvent pas être égale car on aurait alors
d'où
z1
ce qui est impossible avec
Δ
.
4/ Représentation d’un nombre complexe par un vecteur du plan
A partir de tout nombre complexe :
Il est possible de construire un vecteur
du plan de coordonnées
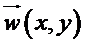pour cela, il faut tout d'abord doter le plan d'une base, qui ne sera pas notée
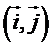mais
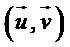pour éviter toute confusion avec i .
Pour pouvoir plus tard utiliser le théorème de Pythagore, on prend une base orthonormée.
Exemple
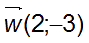représente le nombre complexe : 2 - 3i
2 - 3i est appelé affixe du vecteur
ce qui se note : 
5/ Propriétés de l’affixe d’un vecteur
A tout nombre complexe correspond un unique vecteur du plan dans une base donnée.
Ce qui d'un point de vue pratique s'utilise de la sorte :
Si deux vecteurs sont égaux alors ils ont même affixe.
Reciproquement :
Si deux vecteurs ont même affixe alors ils sont égaux.
Voici maintenant, quelques propriétés sur les affixes de vecteurs qui découlent de façon évidente des propriétés connues sur les coordonnées de vecteurs.
L'affixe du vecteur nul est nulle.
L'affixe du vecteur opposé est l'opposée de l'affixe du vecteur.
L'affixe de la somme de deux vecteurs est égale à la somme des affixes de ces deux vecteurs.
En conséquence des propriétés 3 et 4 :
L'affixe de la difference de deux vecteurs est égal à la difference des affixes des deux vecteurs.
Cette propriété est très utilse pour montrer que deux vecteurs son colinéaires.
Attention !
Cette propriété est fausse si k est un nombre complexe non nul.
6/ Représentation d’un nombre complexe par un point du plan
Munissons maintenant notre plan d'un repère orthonormé :
- une origine.
- une base orthonormée.
A partir de tout nombre complexe :
on peut alors construire un point M du plan de coordonnées (x ; y)
A(4;2) représente le nombre complexe : 4 + 2i .
4 + 2i est appelé affixe du point A.
A est appélé image de 4 + 2i .
7/ Plan complexe, cas particuliers
A tout nombre complexe, correspond un unique point du plan dans un repère donné.
On a donc l'application suivante :
Ce plan où chaque point represente un nombre complexe est appelé : Plan complexe
Cas particuliers :
On a donc l'application suivante : 
Plus généralement les points images de nombres réels ont une ordonnée nulle et sont donc situés sur l'axe des abscisses.
C'est pourquoi cet axe est appelé axe des réels.
un autre cas particulier : 
On a donc l'application suivante : 
Plus généralement : les points images de nombres réels ont une ordonnée nulle et sont donc situés sur l'axe des ordonnée
C'est pourquoi cet axe est appelé axe des imaginaires purs
Et conséquence :
0 étant réel et imaginaire pur,son image est sur les deux axes,c’est l’origine du repère.
z0 = 0
A tout nombre complexe, correspond un unique point du plan dans un repère donné.
8/ Propriétés de l’affixe d’un point
A tout complexe, correspond un unique point du plan dans un repère donné.
Ce qui d'un point de vue pratique s'utilise de la sorte :
Si deux points sont confondus alors ils ont même affixe.
Reciproquement :
Si deux points ont même affixe alors ils sont confondus.
Ce qui d'un point de vue pratique s'utilise de la sorte :
Maintenant quelques propriétés sur les affixes de points qui découlent de façon évidente des propriétés connues sur les coordonnées de points.
Formule que les élèves n'arrivent pas à assimiler alorsqu'elle est très simple à retenir en français :
l'affixe du barycentre est la moyenne pondérée des affixes.
Attention !
Ne pas oublier qu'une équivalence peut s'utiliser dans les deux sens !
9/ Image du conjugué
10/ Lien entre affixe d’un point et affixe d’un vecteur
Par définition, les coordonnées du point M dans le repère
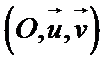sont les coordonnées du vecteur
dans la base
.
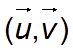et M ayant les même coordonnées ils ont donc la même affixe.
Dans le plan complexe de repère
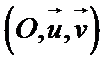
Conséquence :
En effet 
Remarque
Cette formule peut evidemment aussi se demontrer en utilisant la formule des coordonnées du vecteurs.
Pour retenir cette formule :
