.gif)
.gif)
.gif)
Angles
Cours maths 6ème
Angles : On revoit la notion d’angle en précisant le vocabulaire : angles aigus, obtus, droits, plats, saillants, rentrants. On aborde la mesure des angles en introduisant le degré comme unité d’angle et le rapporteur comme un nouvel instrument permettant de déterminer la mesure en degré d’un angle. |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Angle : définitions
Définitions :
Un angle est une portion de plan délimitée par deux
demi-droites ayant la même origine.
Les deux demi-droites s’appellent les côtés de l’angle.
L’origine commune des deux demi-droites s’appelle le sommet de l’angle.
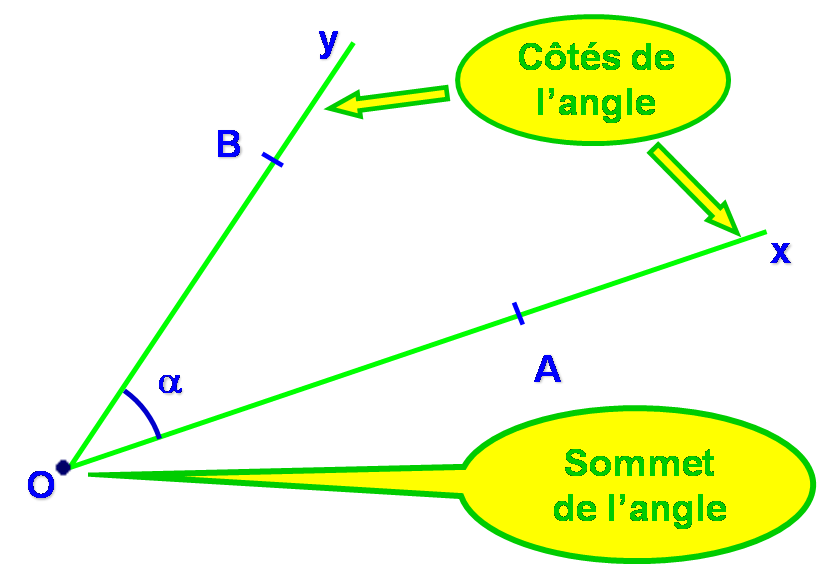
Angle : notations
Cet angle peut être noté :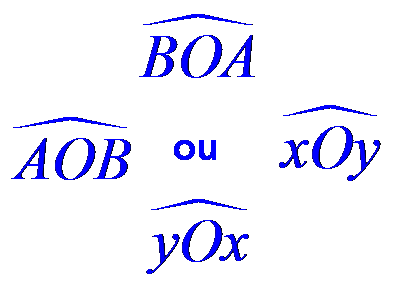
La lettre désignant le sommet de l’angle est toujours placée au milieu.
On peut aussi noter cet angle en utilisant une lettre : ici la lettre α .
α est une lettre de l’alphabet grec qui se prononce « alpha ». C’est l’équivalent du a de notre alphabet.
Angles superposables
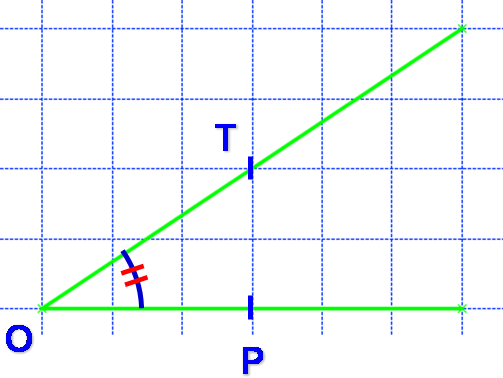
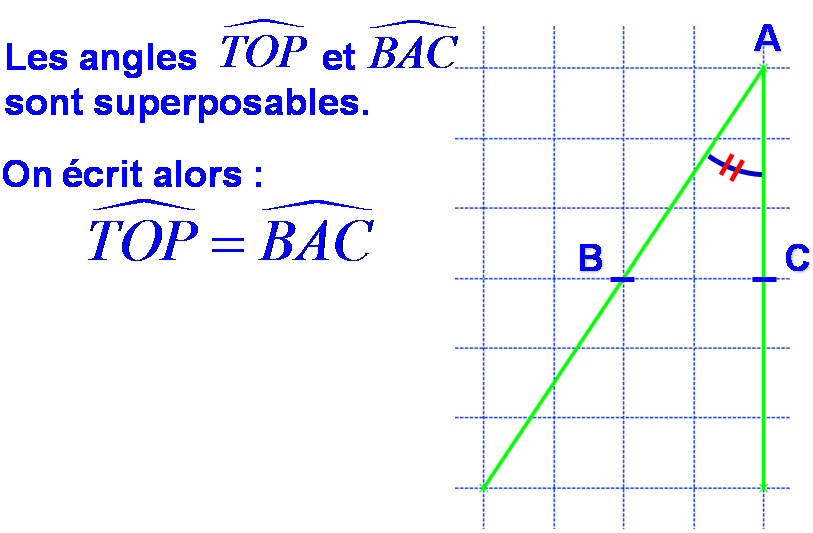
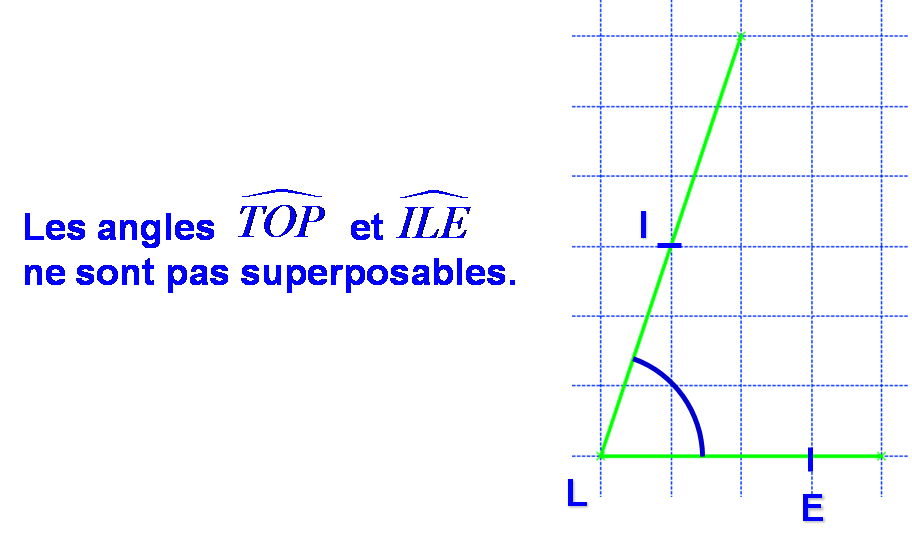
Sur un dessin, on montre que deux angles sont égaux en les marquant avec un symbole identique.
Angles particuliers
Angles aigus - Angles obtus
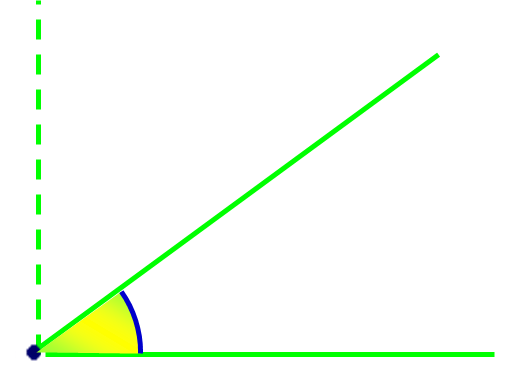
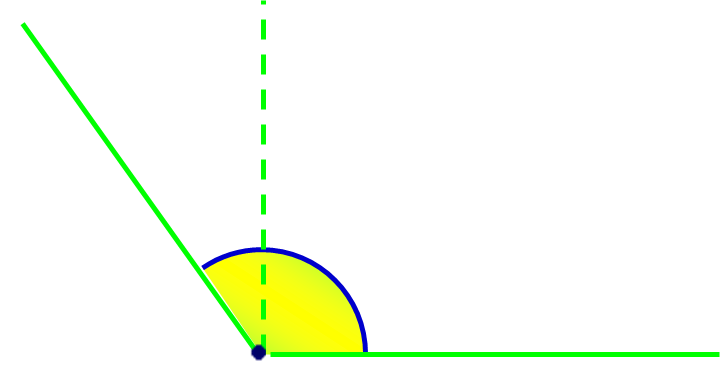
| Un angle aigu est un angle plus petit qu’un angle droit. | Un angle obtus est un angle plus grand qu’un angle droit et plus petit qu’un angle plat. |
Angles saillants
Définition :
Un angle saillant est un angle qui est plus petit qu’un angle plat.
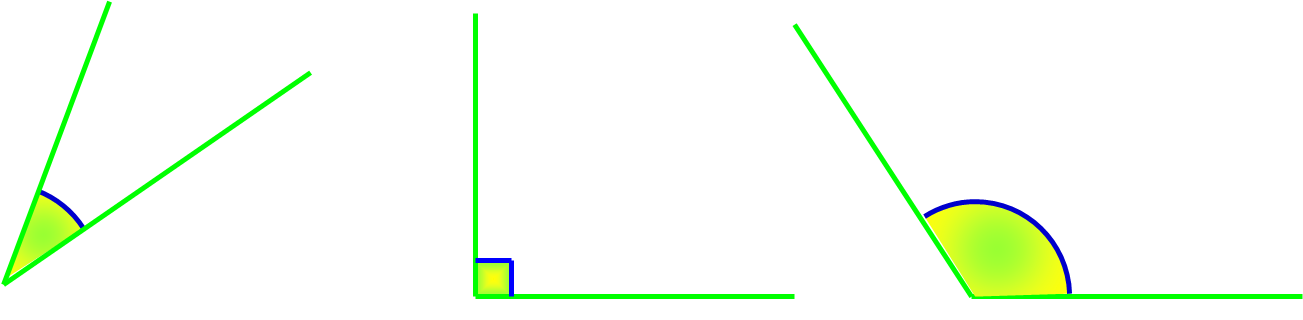
Ces trois angles sont des angles saillants.
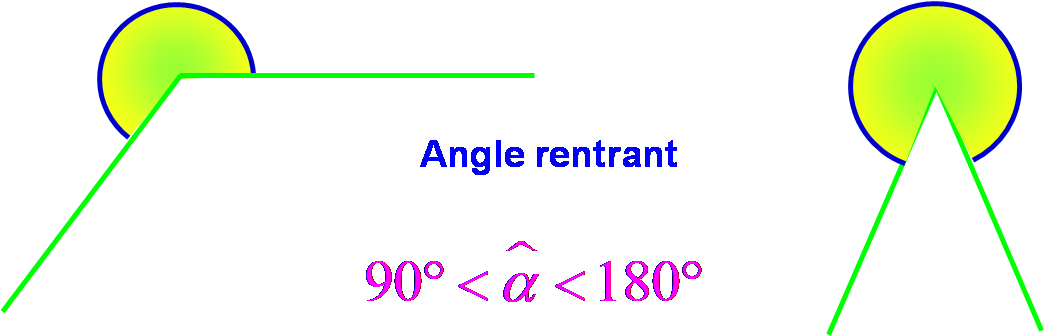
Angles rentrants
Définition :
Un angle rentrant est un angle qui est plus grand qu’un angle plat.
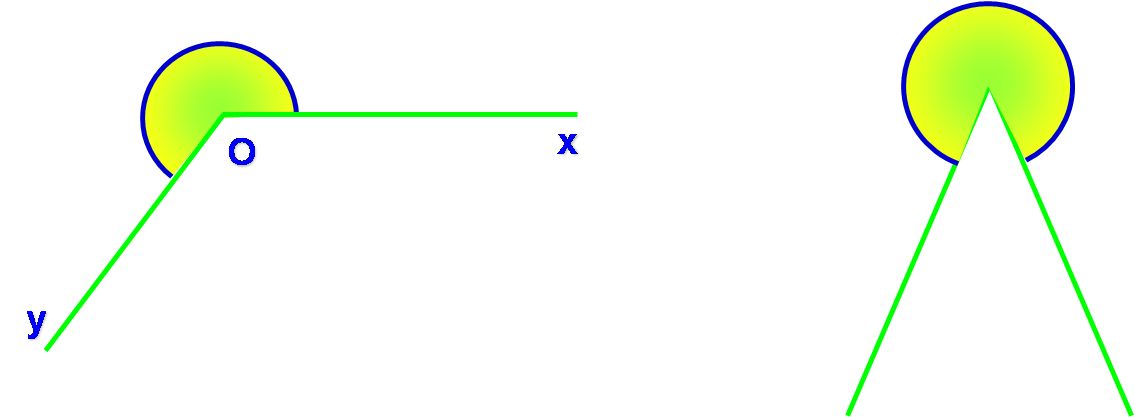
Ces deux angles sont des angles rentrants.
Un angle rentrant est noté :
Mesure d’un angle et rapporteur
Le rapporteur est un instrument qui sert à mesurer des angles.
Il ne s’agit pas d’un instrument de tracé mais d’un instrument de mesure.
Il existe plusieurs unités pour mesurer les angles :
le degré
le grade
le radian
le grade
le radian
Au collège, on utilise uniquement le degré.
Le degré est noté °.
Les rapporteurs sont gradués en degrés (quelques fois aussi en grades) de 0° à 180°.
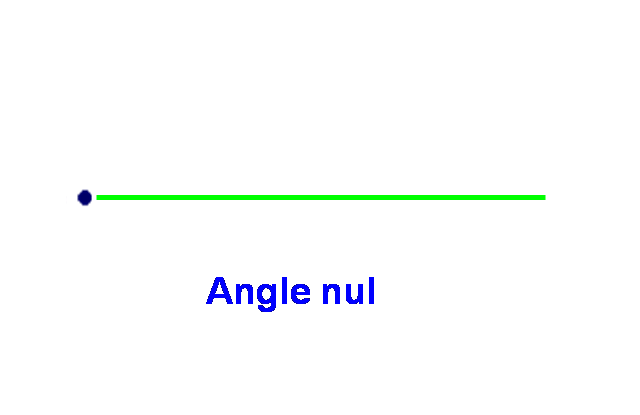
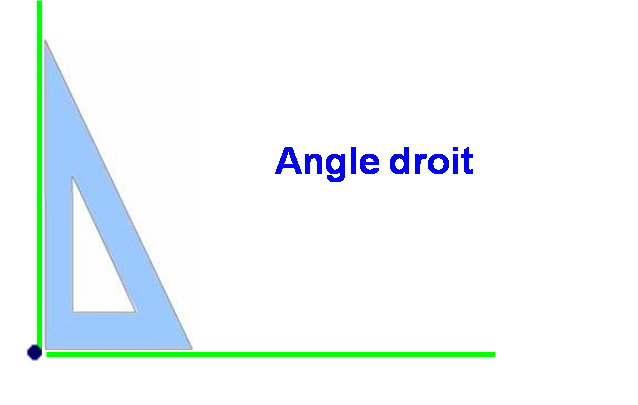
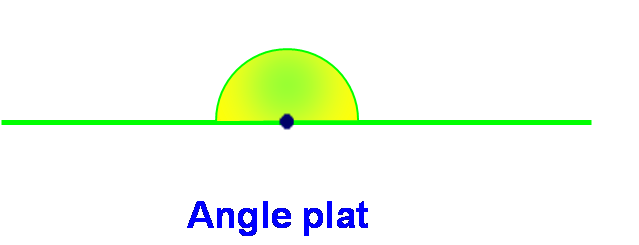
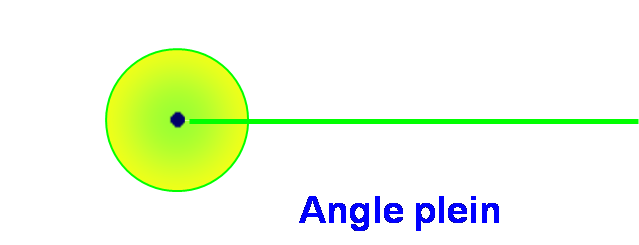
Mesure des angles particuliers
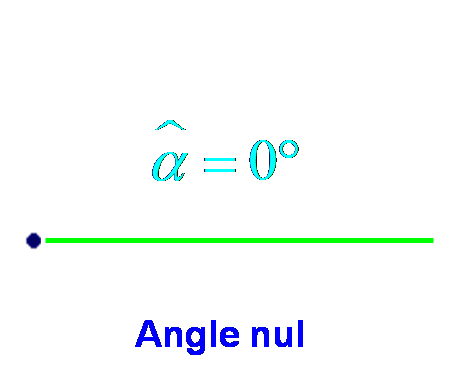
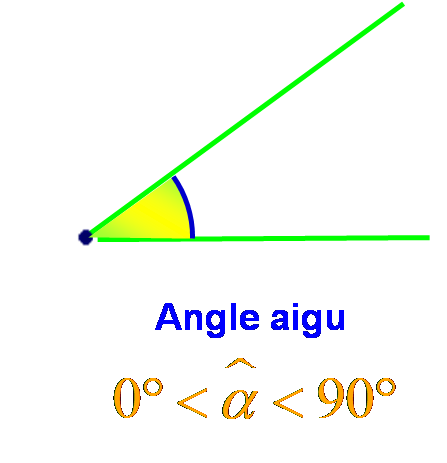
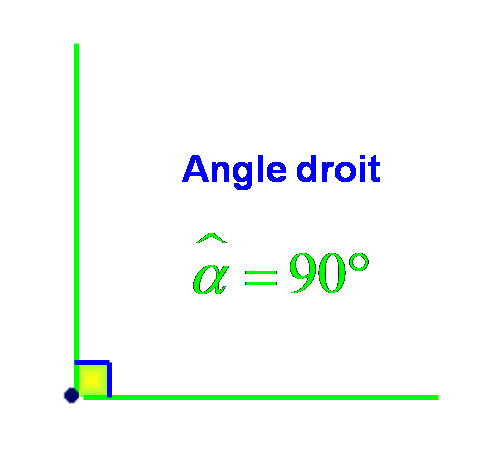
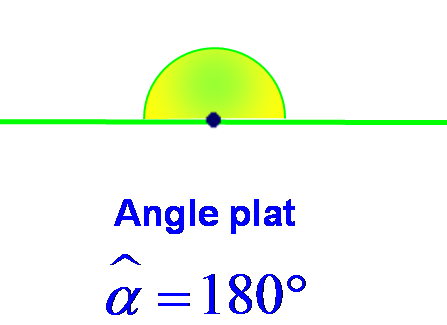
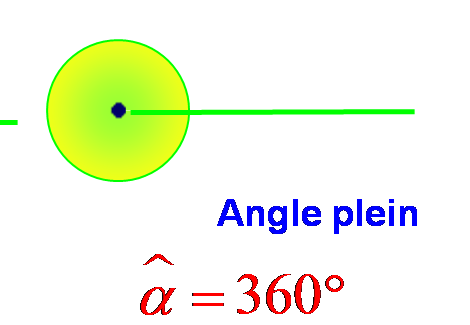
Mesure des angles particuliers
.png)
Mesurer un angle avec un rapporteur
Comment mesurer un angle avec un rapporteur ?
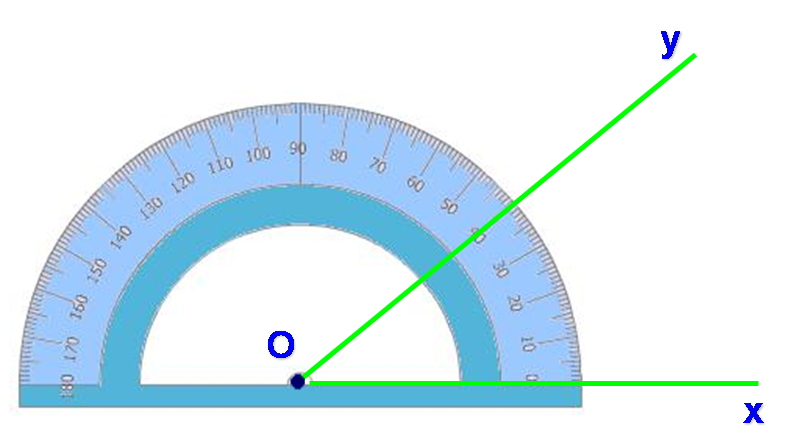
On place le rapporteur sur l’angle :
- le centre du rapporteur doit coïncider avec le sommet de l’angle
- le zéro de la graduation est placé sur l’un des côtés de l’angle
Ensuite on repère le trait de la graduation qui coïncide avec le deuxième côté de l’angle et on lit la mesure de l’angle.
Ici, l’angle 
mesure 40°. ................... 
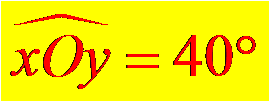
mesure 40°. ................... Construire un angle avec un rapporteur
Comment contruire un angle avec un rapporteur ?
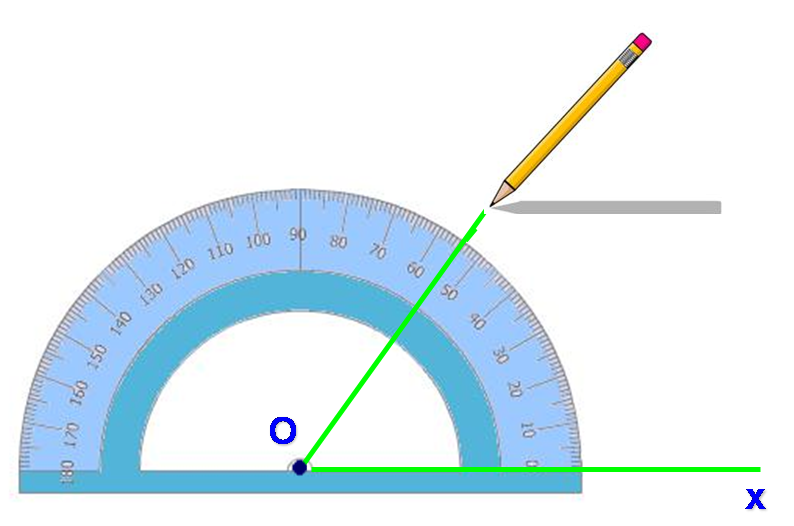
La demi-droite [Ox) est donnée.
On veut construire un angle xÔy qui mesure 55°.
On positionne le rapporteur en plaçant son centre sur le point O et le côté [Ox) sur la graduation 0.
Puis on repère la position de la graduation souhaitée, ici 55°, avec un point.
On retire le rapporteur et on trace la demi-droite [Oy) à l’aide d’une règle.
On a ainsi construit un angle xÔy qui mesure 55°.
Reproduire un angle avec la règle et le compas
.png)
Pour reproduire l’angle xÔy avec une règle et un compas, on commence par tracer une demi-droite [Au).
Puis on trace un arc de cercle de centre O qui coupe [Ox) en E et [Oy) en F.
Avec l’ouverture de compas OE, on trace un arc de cercle de centre A qui coupe [Au) en E’.
Avec l’ouverture de compas EF, on trace un arc de cercle de centre E’ qui coupe l’arc de cercle bleu de centre A en F’.
Avec une règle, on trace la demi-droite [AF’).
On a [AF’) = [Av) et xÔy = uÂv.
Cours complémentaires : |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)