.gif)
.gif)
.gif)
Triangle rectangle - propriétés
Cours maths 3ème
Triangle rectangle - propriétés : Ce cours a pour objectifs de travailler sur la propriété de Pythagore, sa réciproque et les triangles inscrits dans des demi-cercles. Des rappels sur les triangles seront faits en activité. Ce cours permet de consolider et d’approfondir des notions vues en 4ème et peut être suivi dès le début de l’année. |
| ► Sommaire cours maths 3ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Avant de commencer …
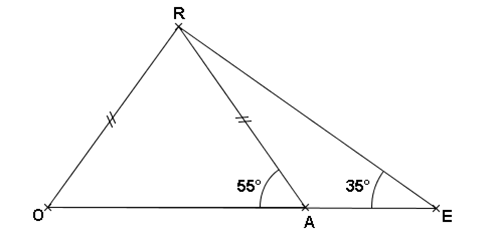
Comment démontrer que les droites (RO) et (RE) sont perpendiculaires ?
On sait que : ROA est un triangle isocèle en R
Or : si un triangle est isocèle, alors ses angles à la base sont égaux
Donc : RÔA = RÂO = 55°
On sait que : dans le triangle ROE, RÔE = 55° et RÊO = 35°
Or : dans tous les triangles, la somme des mesures des trois angles vaut 180°
Donc : ORE = 180 – (55 + 35) = 180 – 90 = 90°.
Conclusion : Les droites (RO) et (RE) sont perpendiculaires.
Enoncé de la propriété :
Si un triangle est rectangle
Alors le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des 2 autres côtés.
A quoi sert cette propriété ?
Cette propriété sert à calculer une longueur dans un triangle rectangle.
Exemple :
On sait que ABC est un triangle rectangle en A.
D’après le théorème de Pythagore, on a :
BC² = AC² + AB²
D’après le théorème de Pythagore, on a :
BC² = AC² + AB²
Applications du théorème de Pythagore :
Dans chacun des cas suivants, appliquer le théorème de Pythagore :
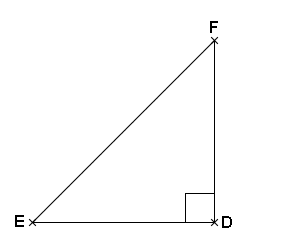
On sait que DEF est un triangle rectangle en D.
D’après le théorème de Pythagore, on a :
EF² = DE² + DF²
D’après le théorème de Pythagore, on a :
EF² = DE² + DF²
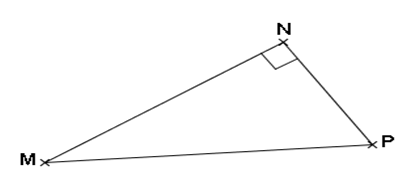
On sait que MNP est un triangle rectangle en N.
D’après le théorème de Pythagore, on a :
MP² = MN² + NP²
D’après le théorème de Pythagore, on a :
MP² = MN² + NP²
Réciproque du théorème de Pythagore
Enoncé de la réciproque :
Dans un triangle,
Si le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des 2 autres côtés
Alors le triangle est rectangle
A quoi sert cette propriété ?
Cette propriété sert à montrer qu’ un triangle est rectangle.
Exemple : Montrer que ABC est un triangle rectangle.
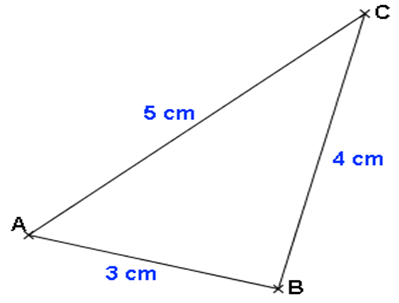
On choisit le plus long côté : [AC]
AC² = 5² = 25
AB² + BC² = 3² + 4² = 9 + 16 = 25
AC² = AB² + BC²
Donc, d’après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
AC² = 5² = 25
AB² + BC² = 3² + 4² = 9 + 16 = 25
AC² = AB² + BC²
Donc, d’après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
Triangle inscrit dans un cercle
Propriété :
Si un triangle est inscrit dans un cercle et que l’un des côtés du triangle est un diamètre du cercle
Alors le triangle est rectangle.
A quoi sert cette propriété ?
Cette propriété sert à montrer qu’ un triangle est rectangle.
Exemple : Montrer que ABC est un triangle rectangle.
.png){kind=small}
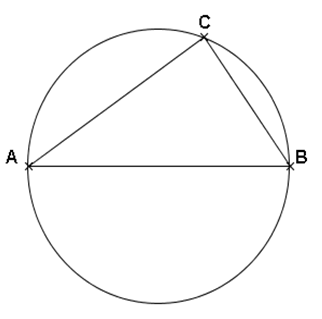
On sait que :
ABC est inscrit dans le cercle de diamètre [AB].
Or :
Si un triangle est inscrit dans un cercle et que l’un des côtés du triangle est un diamètre du cercle, alors le triangle est rectangle.
Donc :
ABC est un triangle rectangle en C.
Cours complémentaires : |
| ► Sommaire cours maths 3ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)