Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Théorème de Thalès - sens direct
Ce cours a pour objectifs de faire travailler la propriété de Thalès sous ses différentes configurations et d’apprendre à placer des points sur une droite graduée.
J’ai déjà vu en 4ème…
En 4ème, j’ai appris à calculer une longueur dans un triangle coupé par une parallèle.
Exemple :
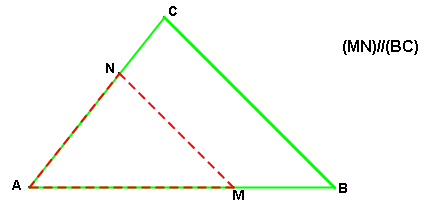
On sait que :
♦ Les points A, M, B sont alignés, ainsi que les points A, N et C
♦ Les droites (MN) et (BC) sont parallèles
On peut donc utiliser le théorème de Thalès :
Remarque :
Le triangle AMN est une réduction du triangle ABC.
L’échelle est :
Activité : Des figures connues
Des figures connues : ABC et AMN sont « emboités »
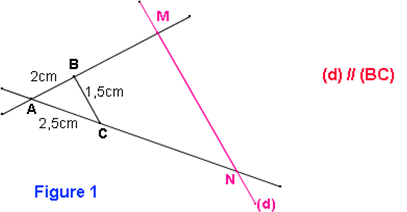
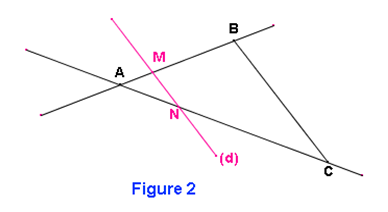
Sur la figure 1, AM = 4cm. Calculer AN et MN
AM = AB×2
D’où AN = 2,5×2 = 5cm et MN = 1,5×2 = 3cm.
Activité : Configuration du papillon
Une figure nouvelle : ABC et AMN sont « opposés par le sommet »
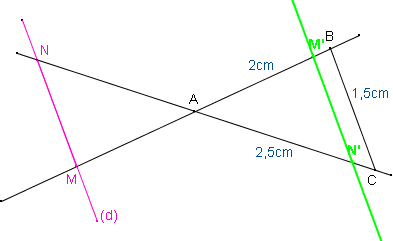
1) Par la symétrie de centre A, on construit les symétriques M’ de M et N’ de N.
Que peut-on dire des droites (M’N’) et (BC)? Pourquoi ?
On sait que :
les points M et M’ sont symétriques par rapport à A
les points N et N’ sont symétriques par rapport à A
Donc :
les droites (MN) et (M’N’) sont symétriques par rapport à A
Or :
si deux droites sont symétriques par rapport à un point, alors elles sont parallèles
Donc :
(MN) // (M’N’)
On sait que :
(MN) // (BC) et (MN) // (M’N’)
Or :
si deux droites sont parallèles, alors toute parallèle à l’une est parallèle à l’autre
Donc :
(BC) // (M’N’)
2) Montrer que :
On sait que :
Les points A, M’, B sont alignés, ainsi que les points A, N’ et C
Les droites (M’N’) et (BC) sont parallèles
On peut donc utiliser le théorème de Thalès :
Or :
par symétrie centrale, on a : AM = AM’ , AN = AN’ et MN = M’N’
Donc :
Théorème de Thalès
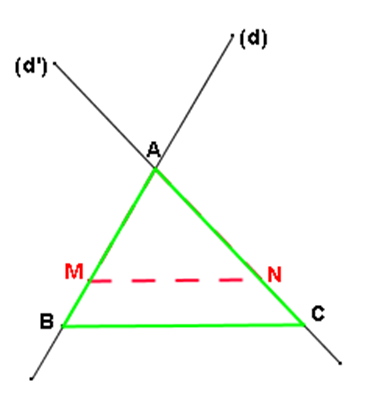
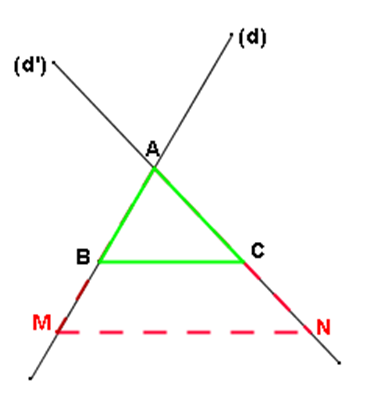
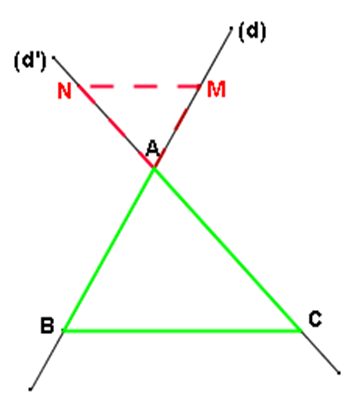
Enoncé du théorème de Thalès :
Soient (d) et (d’) deux droites sécantes en
A.
Soient
B et
M deux points de (d) distincts de
A.
Soient
C et
N deux points de (d’) distincts de
A.
Si les droites (
BC) et (
MN) sont parallèles, alors :
A quoi sert ce théorème ?
Ce théorème sert à calculer une longueur.
Exemple d’application du théorème de Thalès
Exemple :
(BC) et (MN) sont parallèles
AB = 6 cm ; AC = 8,4 cm ;
AM = 4 cm et MN = 3 cm.
Calculer AN puis BC.
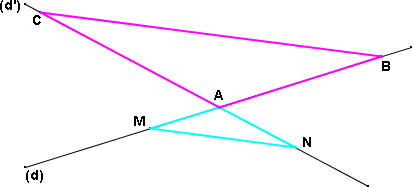
On sait que :
les points M,A, B sont alignés ainsi que les points N,A, C les droites ( MN) et ( BC) sont parallèles.
D’après le théorème de Thalès, on a :
D'après les données de l'énoncé, on a :
Cours complémentaires
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.