Cours maths 5ème

Symétrie centrale - propriétés

A partir de quelques propriétés admises ou démontrées concernant les points alignés, les droites, les demi-droites, un premier pas sera fait vers la formulation d’une démonstration. Les propriétés du centre de symétrie d’une figure seront ensuite étudiées.

Points alignés

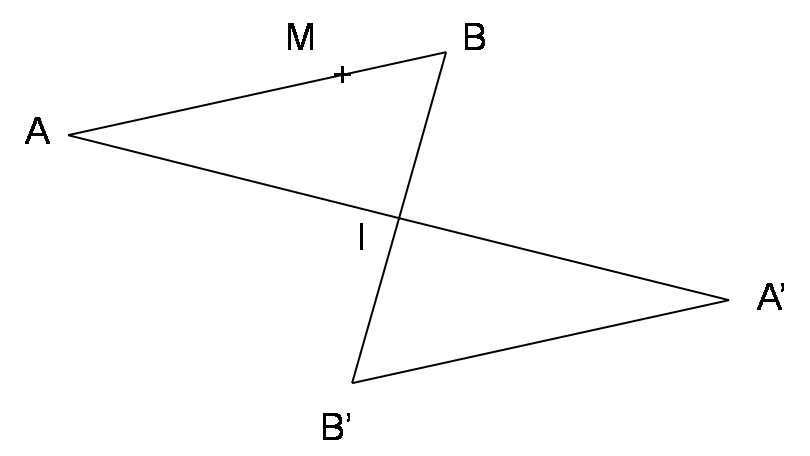A, B et I sont trois points du plan.
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.

M est un point sur le segment [AB].

Points alignés et leurs symétriques

A, B et I sont trois points du plan.
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.
M est un point de [AB]
Les points A, B et M sont alignés.

On appelle M’ le symétrique de M par rapport à I. M’ est sur la demi-droite [MI).

Peut on affirmer que M’ est un point de [A’B’] ?

 

 

A, B et I sont trois points du plan.
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.
M est un point de [AB] et M’ est le symétrique de M par rapport à I.

Le symétrique du triangle ABI par rapport à I est le triangle A’B’I

M étant un point situé sur le côté [AB] du triangle ABI, lors du demi-tour autour de I, la figure est conservée dans son ensemble.
M’ est donc bien un point du segment [A’B’].

 

Propriété de symétrie centrale

Trois points alignés ont pour symétriques par rapport à un point I trois points alignés.

 

Droites symétriques

(d) est une droite et I un point du plan qui n’est pas un point de la droite (d).

On appelle (d’) la droite symétrique de (d) par rapport à I.
On veut comparer (d) et (d’).

Sur la droite (d), on donne un point A quelconque et le point B tel que (IB) ⊥ (d).

On va construire les points A’ et B’symétriques respectifs de A et B par rapport à I

 

 

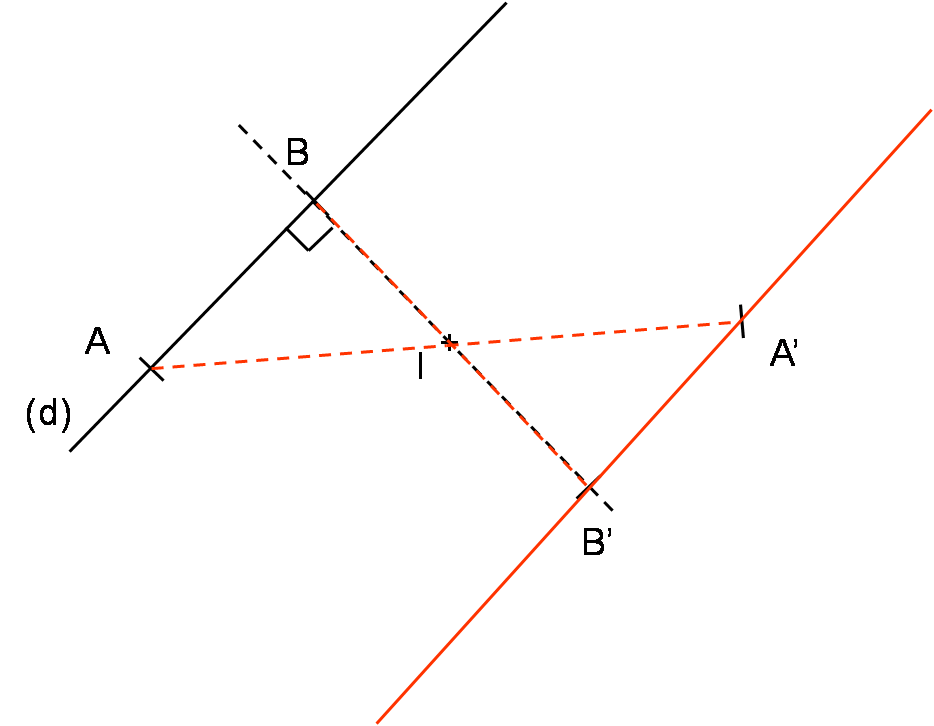(d) est une droite et I un point du plan.
(d’) est la droite symétrique de (d) par rapport à I.
A est un point quelconque de (d) et B est le point de (d) tel que (IB) ⊥ (d).
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.

Comment peut-on aussi nommer (d’) ?
Quel est le symétrique de l’angle ABI ?
Quelle est sa mesure ?

 

 

(d) est une droite et I un point du plan.
(d’) est la droite symétrique de (d) par rapport à I.
A est un point quelconque de (d) et B est le point de (d) tel que (IB) ⊥ (d).
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.
La droite (d’) est en fait la droite (A’B’).

Le symétrique de l’angle ABI est l’angle A’B’I.
Ces deux angles ont la même mesure.
Comment les points B, I et B’ sont-ils disposés ?
Comment sont les droites (BB’) et (d’) ?

 

 

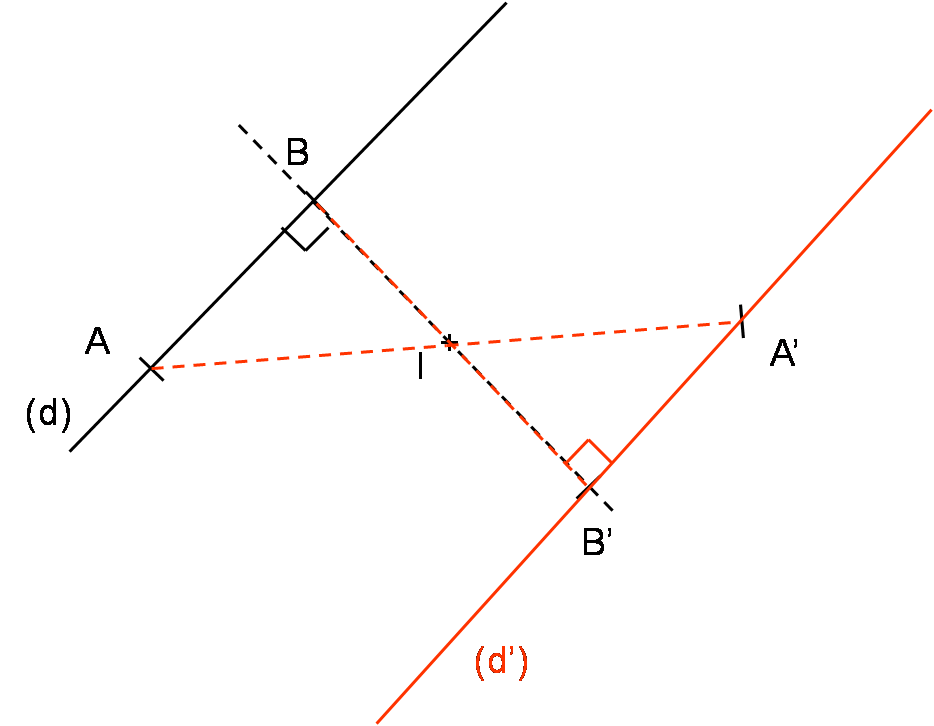(d) est une droite et I un point du plan.
(d’) est la droite symétrique de (d) par rapport à I.
A est un point quelconque de (d) et B est le point de (d) tel que (IB) ⊥ (d).
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.
Les points B, I et B’ sont alignés.

Les droites (BB’) et (d’) sont donc perpendiculaires.

Que peut on en conclure pour les droites (d) et (d’) ?

 

 

(d) est une droite et I un point du plan.
(d’) est la droite symétrique de (d) par rapport à I.
A est un point quelconque de (d) et B est le point de (d) tel que (IB) ⊥ (d).
A’ et B’ sont les symétriques respectifs de A et de B par rapport à I.

(BB’) ⊥ (d)
(BB’) ⊥ (d’)

Deux droites perpendiculaires à la même troisième sont parallèles entre elles.

Conclusion : (d) // (d’)

 

Droites symétriques : propriété

Deux droites symétriques par rapport à un point sont parallèles.

 

Demi-droites symétriques : activité

A, B et I sont trois points du plan non alignés.
A’ et B’ sont les symétriques respectifs de A et B par rapport à I.

En bleu est tracé la demi-droite [AB).

En rouge, le tracé du symétrique de la demi-droite [AB).

 

Demi-droites symétriques : propriété

Deux demi-droites symétriques par rapport à un point sont parallèles et de sens contraire.

 

Centre de symétrie d’une figure

Quand une figure est son propre symétrique par rapport à un point,-ce point est appelé « centre de symétrie » de la figure.

Le symétrique de la figure ci-contre par rapport au point I, est la même figure...

I est le centre de symétrie de la figure.