.gif)
.gif)
.gif)
Symétrie axiale
Cours maths 6ème
Symétrie axiale : Ce cours permet de découvrir la notion de figures symétriques par rapport à une droite. Il montre comment construire le symétrique d’un point, d’un segment, d’une droite, d’un cercle et met en évidence les propriétés de « conservation » de la symétrie axiale : conservation des distances, de l’alignement, des angles et des aires. |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
Figures symétriques
Définition : Deux figures sont dites symétriques par rapport à une droite (d) si elles se superposent par pliage le long de la droite (d).
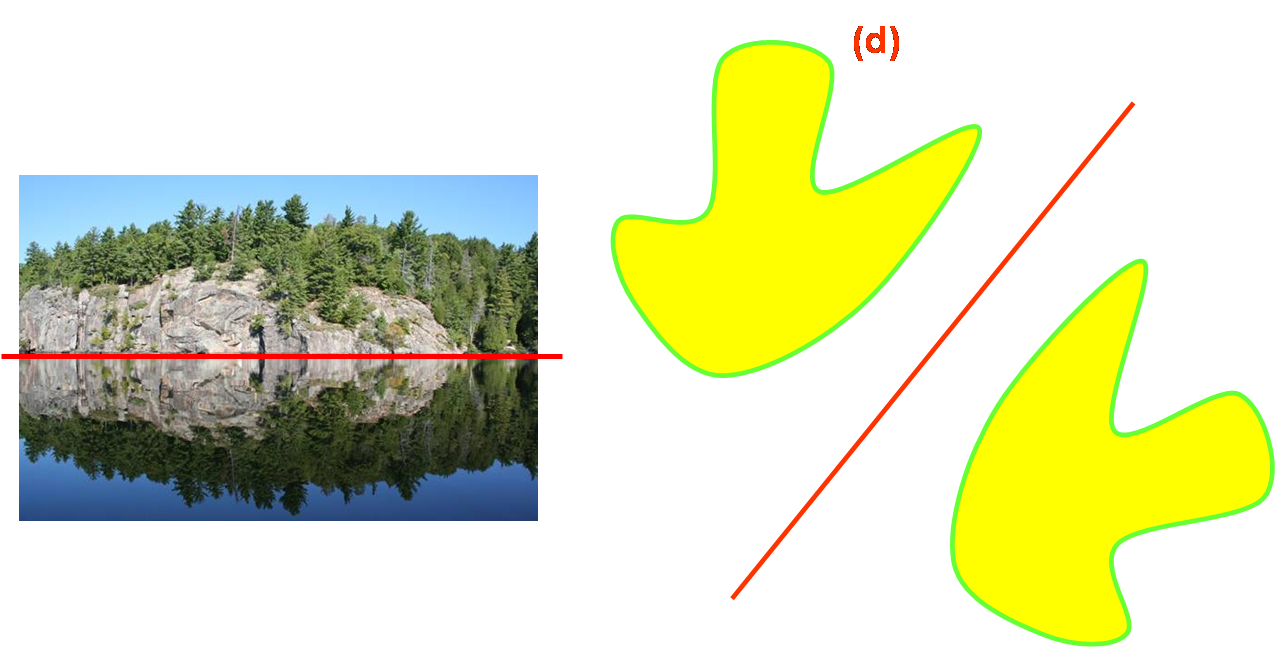
Les figures F1 et F2 se superposent par pliage le long de la droite (d).
Les figures F1 et F2 sont symétriques par rapport à la droite (d).
Les figures F1 et F2 sont symétriques par rapport à la droite (d).
Vocabulaire
La symétrie par rapport à une droite est appelée symétrie orthogonale par rapport à cette droite ou symétrie axiale.
La droite est appelée axe de la symétrie.
Symétrique d’un point
Deux points A et A’ sont symétriques par rapport à une droite (d) s’ils se superposent par pliage le long de cette droite.
Définition : On dit que le point A’ est le symétrique du point A par rapport à une droite (d) si la droite (d) est la médiatrice du segment [AA’].
Remarque :
Si le point A appartient à la droite (d), alors A et A’ sont confondus.
Dans ce cas, A est son propre symétrique par rapport à (d).
Construction du symétrique d’un point
Première méthode : avec une équerre et un compas
Avec l’équerre, on trace la perpendiculaire à la droite (d) passant par A.
Puis on prolonge le trait avec l’équerre.
Avec le compas on reporte la distance entre le point A et la droite (d) de l’autre côté de la droite.
On obtient ainsi le symétrique A’ du point A par rapport à la droite (d).
.png)
Deuxième méthode : avec le compas seul
On prend deux points distincts M et N de la droite (d).
Avec le compas on trace le cercle de centre M passant par A puis le cercle de centre N passant par A.
Ces deux cercles se coupent en A et aussi en un autre point A’ symétrique du point A par rapport à la droite (d).
Symétrique d’un segment
Propriété :
Le symétrique d’un segment par rapport à une droite (d) est un segment de même longueur.
A’ est le symétrique de A par rapport à (d).
B’ est le symétrique de B par rapport à (d).
Le segment [A’B’] est le symétrique
du segment [AB] par rapport à (d).
B’ est le symétrique de B par rapport à (d).
Le segment [A’B’] est le symétrique
du segment [AB] par rapport à (d).
On a A’B’ = AB
On dit que la symétrie axiale conserve les longueurs.
Symétrique d’une droite
Propriété : Le symétrique d’une droite par rapport à une droite (d) est une droite.
Pour construire le symétrique d’une droite par rapport à un axe, il suffit de construire les symétriques de deux points de la droite par rapport à cet axe.
On choisit deux points quelconques A et B de la droite.
On construit les symétriques de A et B par rapport à la droite (d).
A’ est le symétrique de A par rapport à (d).
B’ est le symétrique de B par rapport à (d).
La droite (A’B’) est la droite symétrique
de la droite (AB) par rapport à (d).
Observons le symétrique de la droite (AB) par rapport à (d) ...
1) Dans le cas où la droite (AB) et la droite (d) sont parallèles
La droite (AB) et la droite (A’B’) sont aussi parallèles.
2) Dans le cas où la droite (AB) et la droite (d) sont perpendiculaires
La droite (AB) et la droite (A’B’) sont confondues.
Symétrie et points alignés
Propriété : Les symétriques de trois points alignés par rapport à une droite (d) sont trois points alignés.
Les points A, B et C sont alignés.
Les points A’, B’ et C’ sont aussi alignés.
On dit que la symétrie axiale
conserve l’alignement.
conserve l’alignement.
Symétrique d’un cercle
Propriété : Le symétrique d’un cercle par rapport à une droite (d) est un cercle de même rayon et dont le centre est le symétrique du centre du premier cercle.
♦ A’ est le symétrique de A par rapport à (d).
♦ C’ est le symétrique du cercle C par rapport à (d).
⇒ Les deux cercles C et C’ ont le même rayon.
Symétrique d’un angle
Propriété :
Le symétrique d’un angle par rapport à une droite (d) est un angle de même mesure.
L’angle BÂC et l’angle B’Â’C’
ont la même mesure.
ont la même mesure.
On dit que la symétrie axiale conserve les angles.
Autre propriété
Deux figures symétriques par rapport à une droite ont la même aire.
Les figures F1 et F2 sont symétriques par rapport à la droite (d).
Les figures F1 et F2 ont la même aire.
A1 = aire(F1) / A2 = aire(F2)
A1 = A2
Les figures F1 et F2 ont la même aire.
A1 = aire(F1) / A2 = aire(F2)
A1 = A2
On dit que la symétrie axiale
conserve les aires.
conserve les aires.
Remarque : Les figures F1 et F2 ont aussi le même périmètre.En effet, la symétrie axiale conserve les longueurs !
Construction du symétrique d’une figure
Pour construire le symétrique d’une figure, on construit les symétriques de plusieurs de ses points et on utilise les propriétés de conservation.
Cours complémentaires : |
| ► Sommaire cours maths 6ème A voir aussi : ► Sommaire par thèmes ► Sommaire par notions |
.jpg)