Similitudes indirectes

 

Une transformation du plan est une similitude
si et seulement si
elle multiplie les distances par un réel k, strictement positif.

Les similitudes conservent les angles géométriques.

On appelle similitude directe toute similitude qui conserve les angles orientés.
Une isométrie directe est appelée un déplacement.

Les homothéties sont des similitudes directes.
Tout déplacement est soit une translation, soit une rotation d’angle non nul

Théorèmes  :

La composée d’une similitude de rapport k et d’une similitude de rapport k’
est une similitude de rapport : k x k’

La réciproque d’une similitude de rapport k est une similitude de rapport

La réciproque d’une isométrie est une isométrie.

• La composée de deux similitudes directes ou de deux similitudes indirectes est une similitude directe.
• La composée d’une similitude directe et d’une similitude indirecte est une similitude indirecte.
• La réciproque d’une similitude directe est une similitude directe.
• La réciproque d’une similitude indirecte est une similitude indirecte.

Théorème  :

Toute similitude indirecte est la composée d’une similitude directe et d’une réflexion.

Notons s_(D) la réflexion d’axe (D).

s et s_(D) sont des similitudes indirectes donc leur composée est une similitude directe s’.

* Nous avons donc :  d’où :
* Or, toute réflexion est sa propre réciproque donc 
* Par conséquent, s s’écrit :  , avec s’ similitude directe.

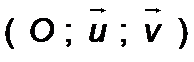
Théorème  : soit s transformation du plan.
Si s est une similitude indirecte de rapport k
alors s admet une écriture complexe de la forme :  avec _la_l = k
Démonstration :
Soit s similitude indirecte de rapport k.

D’après le théorème précédent, quelle que soit la droite (D), s peut s’écrire : où s’ désigne une similitude directe.

Prenons pour (D) l’axe des abscisses, alors s_(D) a pour écriture complexe :  

De plus, d’après un précédent module, s’ similitude directe a une écriture complexe de la forme  : z’ = az + b avec a non nul.

En outre, s’ a pour rapport  _la_l

L’écriture de est donc :

De plus, le rapport de la composée est égal au produit des rapports : k = _la_l x 1 = _la_l

Toute transformation s admettant une écriture de la forme :  avec a ≠ 0 est une similitude indirecte de rapport k = _la_l

Soient M et N points quelconques du plan d’images respectives M’ et N ’ par s.

Alors :
D’où : 
Donc :  , d’où :  M’N’ = _la_l x MN

Et a ≠ 0, donc f est une similitude de rapport k = _la_l

Rajoutons deux points P et Q d’images respectives P’ et Q’.

Nous avons comme précédemment : 

s, transformation du plan, est une similitude indirecte

si et seulement si

s a une écriture complexe de la forme :  avec a ≠ 0

Rappel des résultats vus dans le module de définition des similitudes  :

On appelle point fixe ou point invariant par une transformation, tout point qui a pour image lui-même.

Théorème  : soit s une similitude.

s possède trois points invariants non alignés si et seulement si s est l’identité.

On dira également que toute similitude « fixant » trois points non alignés est l’identité.

Théorème  :

Si deux points distincts A et B sont invariants par une similitude s, alors :
soit s est l’identité, soit s est la réflexion d’axe (AB).

Théorème  :

Un anti-déplacement avec au moins un point invariant est une réflexion.

s ne peut être l’identité car l’identité est un déplacement.

Par conséquent, il existe au moins un point M différent de A qui n’est pas invariant par s.

Comme A = s(A) et que s est une isométrie alors AM’ = AM.

Donc A appartient à la médiatrice de [MM’], qui existe car M et M’ sont distincts.

 et 

donc 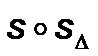 est une similitude qui possède au moins deux points invariants distincts.

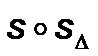est soit l’identité soit une réflexion, or par composition  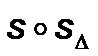est directe.

Donc , d’où  :

► s conserve l’alignement, donc :

- l’image d’une droite est une droite.
- l’image du segment [AB] est le segment [s(A)s(B)] de longueur kAB.
- s conserve les intersections.

► s conserve, de plus, par définition, les rapports de distances donc :

- s conserve le milieu et plus généralement le barycentre.

►  s conserve les angles géométriques, donc :

- s conserve l’orthogonalité et le parallélisme.

►  L’image du cercle de centre O et de rayon r est le cercle de centre s(O) et de rayon kr.
►  s multiplie les aires par k²