Cours de maths à partir de 9.90 €/heure
Cours maths 6ème
Périmètres
On définit la notion de périmètre d’une figure fermée et on le relie à la notion d’unité de longueur. On met en évidence les formules de calcul du périmètre des figures usuelles (rectangle, losange, carré, cerf-volant, cercle) et on introduit le nombre π.
Périmètre d’une figure
Définition Le périmètre d’une figure fermée est la longueur de son contour. Le mot périmètre vient du grec perimetros, formé de peri qui signifie « autour » et de metros qui signifie « mesure ».
Remarque :
Un périmètre s’exprime en unités de longueur (m, cm, km,…)
Calcul du périmètre
Pour calculer le périmètre d’un polygone, on calcule la somme des longueurs de ses côtés.
.png)
Exemple :
Le périmètre P de ce polygone vaut :
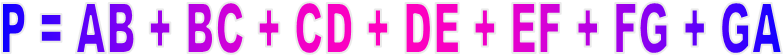
soit
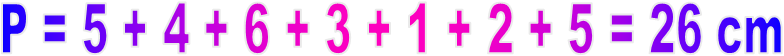
Périmètre du rectangle
Le périmètre d’un rectangle s’exprime en fonction de sa longueur et de sa largeur.
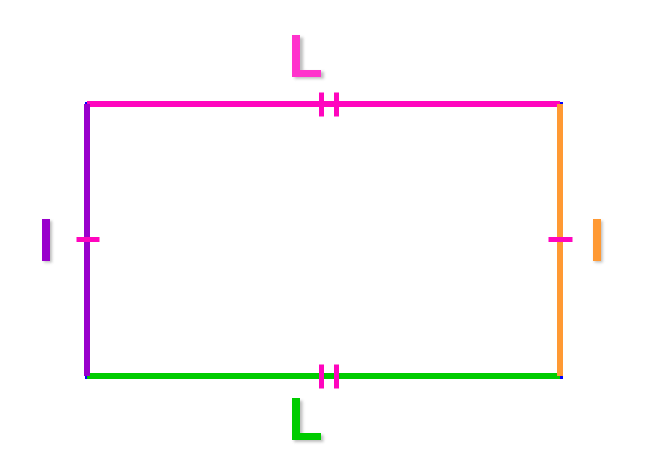
P = L + l + L + l
ainsi ...
P = 2 (L + l)
Périmètre du losange
Les quatre côtés d’un losange ont la même longueur.
Le périmètre d’un losange s’exprime en fonction de la longueur de ses côtés.
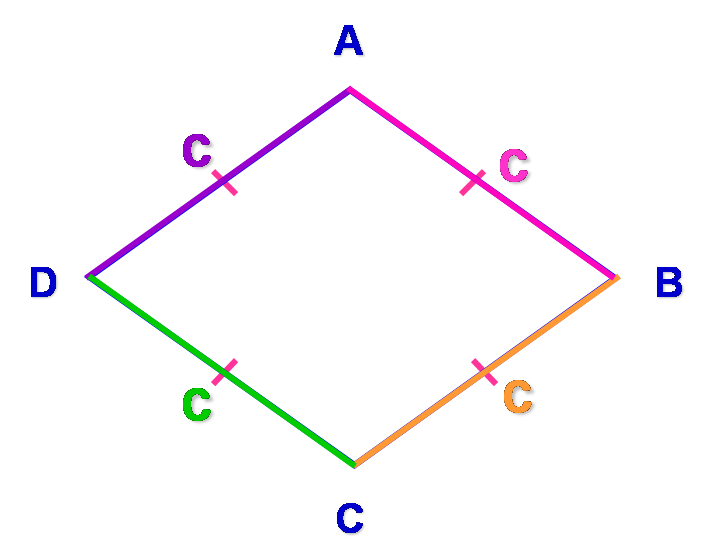
P = c + c + c + c
ainsi ...
P = 4 x C
Périmètre du carré
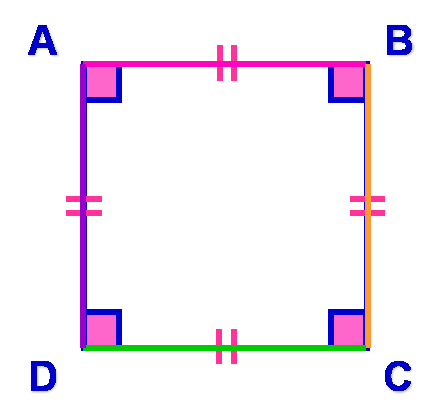
P = c + c + c + c
ainsi ...
P = 4 x C
Périmètre du cerf-volant
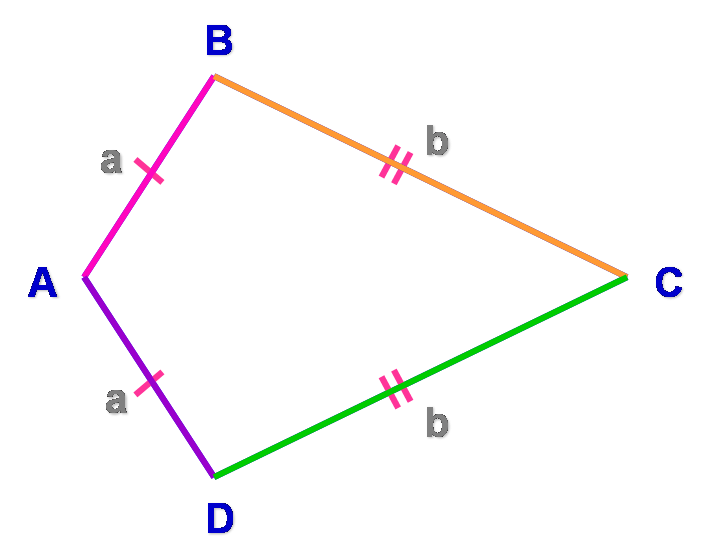
P = a + c + c + a
ainsi ...
P = 2 x (a + b)
Longueur du cercle
Les mesures de la longueur d’un cercle font intervenir un nombre noté π, ce qui se lit « pi » et qui est la première lettre du mot périmètre écrit en grec.
Une valeur approchée du nombre π est 3,14.
π n’est pas un nombre décimal : son écriture ne se termine pas.
Ses premières décimales sont :


Longueur du cercle
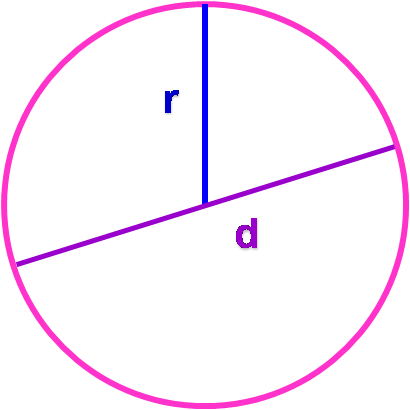
La longueur d’un cercle de rayon r vaut :

Remarque : La longueur d’un cercle peut aussi s’exprimer en fonction du diamètre du cercle.
Si d est le diamètre du cercle, la longueur du cercle vaut : 
Longueur du cercle

La longueur d’un cercle de rayon 4 cm vaut :

Une valeur approchée de P est : 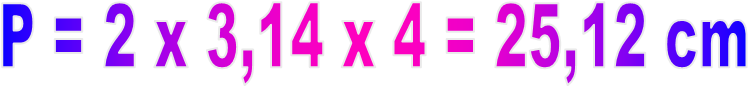
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.