Cours de maths à partir de 9.90 €/heure
Cours maths Terminale S
Intégration - aires et volumes
Ce dernier module traitant de la notion d’intégration commence par des rappels concernant les propriétés, définitions et méthodes vues dans les deux autres modules.
1/ Bases avant intégration
► Notion d'une aire
Définition :
Soit le repère
orthogonal L ’
unité d’aire est l’aire du rectangle OIKJ et se note
u.a.
Dans le cas du repère
1 u.a. = 1 x 2 = 2 cm2
► Intégrale d'une fonction continue positive
Définition :
Soit f fonction continue positive sur un intervalle [ a ; b ] ( avec a < b ).
Et soit X sa représentation dans le repère
L’intégrale de la fonction f sur [ a ; b ] notée est en
unités d’aire, l’aire de la partie du plan limitée par :
Propriétés :
= 0
Si f est nulle sur [ a ; b ] alors : = 0
► Intégrale d’une fonction continue négative
Définition :
Soit f fonction continue négative sur un intervalle [ a ; b ] ( avec a < b ).
Et soit X sa représentation dans le repère
L’intégrale de la fonction f sur [ a ; b ] notée
est en
unités d’aire, l’opposé de l’aire de la partie du plan limitée par :
► Intégrale d’une fonction continue
Définition :
Soit f fonction continue sur un intervalle [ a ; b ] ( avec a < b ).
Et soit X sa représentation dans le repère
L’intégrale de la fonction f sur [ a ; b ] notée est en
unités d’aire, la différence entre : les aires situées au dessus de (Ox) et les aires situées en dessous de (Ox).
Théorème :
Soit f fonction continue sur un intervalle I de R.
Et soit a réel, appartenant à I.
La fonction F définie pour tout x de I par :
est l’unique primitive de f sur I qui s’annule en a.
Conséquence :
Soit f fonction continue sur un intervalle I de R et soit F une primitive de f sur I.
Alors, quels que soient a et b appartenant à I :
Le nombre F (b) - F (a) est noté avec des crochets :
Propriétés pratiques : pour toute constante k :
► Propriétés de linéarité :
soient f et g fonctions continues sur l’intervalle [ a ; b ]
L’intégrale de la somme est égale à la somme des intégrales.
Pour toute constante réelle k :
Conséquence des deux propriétés :
l’intégrale de la différence est égale à la différence des intégrales.
► Relation de Chasles :
soit f continue sur un intervalle I et soient a, b et c éléments de I.
► Positivité de l’intégrale :
Soit f fonction continue sur l’intervalle [ a ; b ].
Si pour tout x élément de [ a ; b ] : f (x) > 0 alors :
Autrement dit : « l’intégrale d’une fonction positive est positive ».
Et également : «l'intégrale d'une fonction négative est négative»
Conséquence n° 1:
soient f et g fonctions continues sur l’intervalle [ a ; b ].
Si pour tout x élément de [ a ; b ] : f (x) < g (x)
alors :
Conséquence n° 2 : Inégalité de la moyenne.
Soit f fonction continue sur l’intervalle [ a ; b ].
S’il existe deux réels m et n tels que pour tout x de [ a ; b ] : m < f (x) < M
alors :
► Théorème : intégration par parties
Si u et v sont deux fonctions dérivables sur un intervalle I,
et si leurs dérivées u’ et v’ sont continues sur I, alors,
quels que soient a et b éléments de I :
2/ Valeur moyenne d’une fonction
Définition : soit f fonction continue sur l’intervalle [ a ; b ].
La valeur moyenne de la fonction f sur l’intervalle [ a ; b ] est le réel défini par :
illustration graphique :
prenons l’exemple d’une fonction continue positive sur [ a ; b ].
Alors :
est en unités d’aire, l’aire de la surface située
entre (C), l’axe (Ox) et les droites d’équations x = a et x = b est l’aire du rectangle hachuré.
et correspond à avec g fonction constante sur [ a ; b ] égale à K.
Pour K = m : on a
m correspond donc à la valeur de K pour laquelle
l’aire du rectangle est égale à l’aire située sous la courbe.
Une fonction constante ayant pour valeur cette
« valeur moyenne » sur l’intervalle [ a ; b ]
aura la même intégrale que f.
Du strict point de vue de l’intégrale, f vaut donc,
en moyenne, cette valeur sur l’intervalle [ a ; b ].
3/ Calcul d’aire : surface limitée par deux courbes
Soit le repère orthogonal
Théorème : soient f et g fonctions continues sur l’intervalle [ a ; b ].
Soit A l’aire de la surface délimitée par la courbe de f et la courbe de g,
l’axe de abscisses, et les droites d’équation : x = a et x = b.
Si pour tout x de [ a ; b ], on a f (x) < g alors : A=
Ce théorème évident du point de vue graphique dans le cas de deux fonctions positives est donc également valable dans le cas général.
Sa démonstration est ici admise.
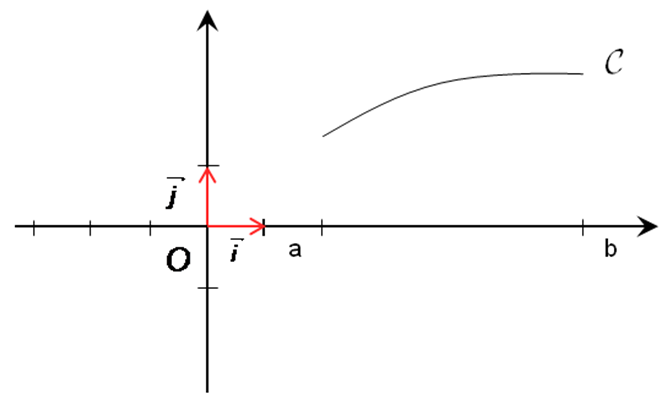
4/ Aires et volumes
Soit f fonction continue sur l’intervalle [ a ; b ].
Et soit X sa représentation dans le repère
Appelons A, l’aire de la surface orange située sous la courbe et mesurée en unités d’aire.
l’aire du petit rectangle vert est
f(x) x dx
La surface orange peut être « quasiment » recouverte par des rectangles de ce type avec x allant de a à b.
Plus l’écart dx sera petit et plus la somme br> des aires des rectangles sera proche de A.
Autrement dit, la somme des f(x)dx tend vers A quand dx tend vers 0, pour x allant de a à b.
Cette limite de somme est notée avec un grand s étiré : qui se lit
intégrale.
Cette égalité entre aire et limite de somme se note dans sa globalité : A =
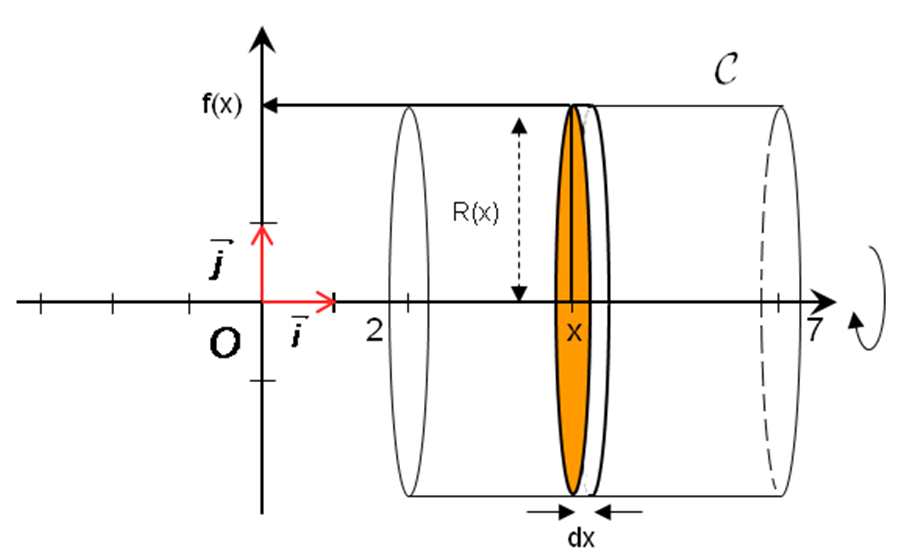
Ce même principe de raisonnement peut être appliqué aux calculs de volumes.
En faisant pivoter la courbe de f autour de l’axe (Ox), on engendre un solide de révolution.
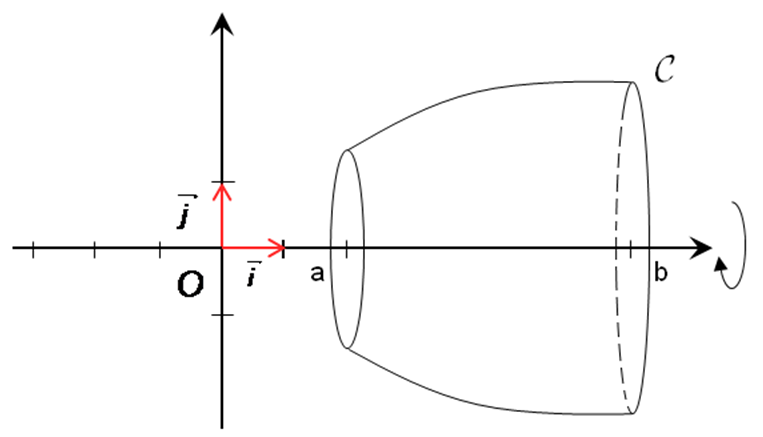
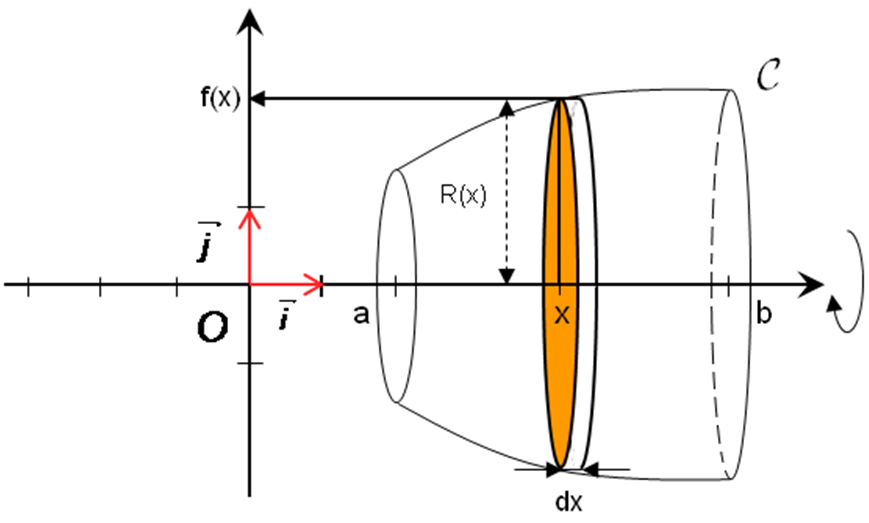
Appelons , le volume de ce solide. Le volume du petit cylindre orange est
L’intérieur du solide peut être « quasiment » rempli par des cylindres de ce type avec x allant de a à b.
Plus l’écart dx sera petit et plus la somme des volumes des cylindres sera proche de
Autrement dit, la somme des tend versquand dx tend vers 0, pour x allant de a à b.
Cette limite de somme est notée avec un grand s étiré :
et on a donc
Or : R (x) = f (x) donc
Théorème :
Soit f fonction continue sur un intervalle [ a ; b ].
En faisant pivoter la courbe de f autour de l’axe (Ox),
on engendre un solide de révolution, dont le volume est :
Remarques :
1) Cette formule est souvent rappelée dans les énoncés de BAC.
2) Il vaut mieux savoir retrouver cette formule plutôt que de l’apprendre.
On sera alors capable de trouver le volume de solides engendrés par rotation autour d’autres axes.
Exemple : volume d’un cylindre
Soit f fonction constante sur l’intervalle [ 2 ; 7 ] définie par f (x) = 2,5
La rotation de la courbe de f engendre un cylindre.
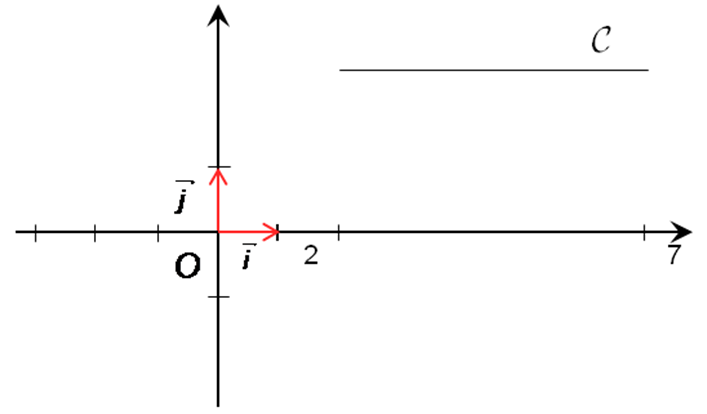
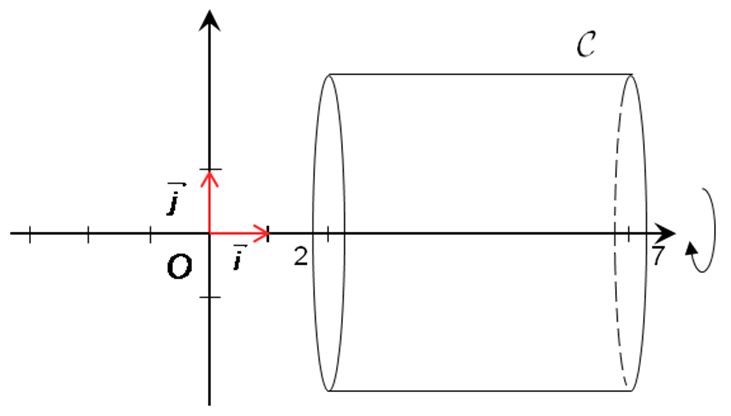
Et x est compris entre 2 et 7 donc :

Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.