Cours maths 5ème
Inégalité triangulaire
Ce cours a pour but, dans un premier temps, de mettre en évidence à travers des activités guidées que le chemin le plus court d’un point à un autre est le segment qui les joint, tout autre trajet étant plus long. L'exposition de ce premier concept permettra de déduire l’inégalité triangulaire et une façon de savoir si 3 longueurs données peuvent être les longueurs des côtés d’un triangle.
Des chemins différents
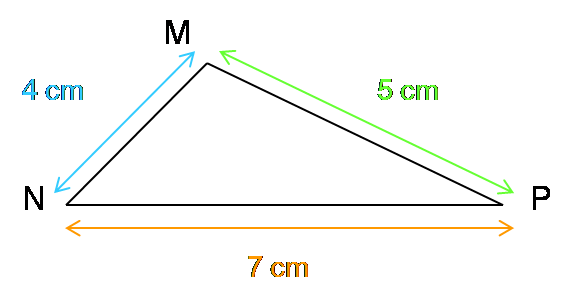Evaluer les longueurs :
MN et MP + PN
MP et MN + NP
NP et NM + MP
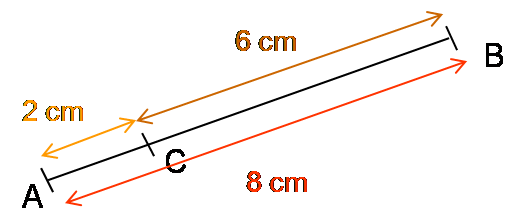Evaluer les longueurs :
AC et AB + BC
BC et BA+ AC
AB et AC + CB
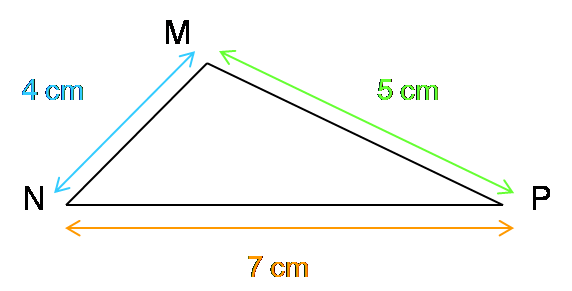On a :
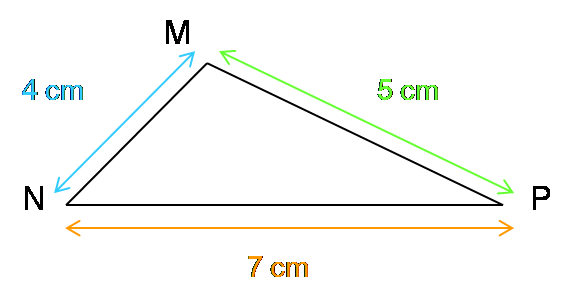
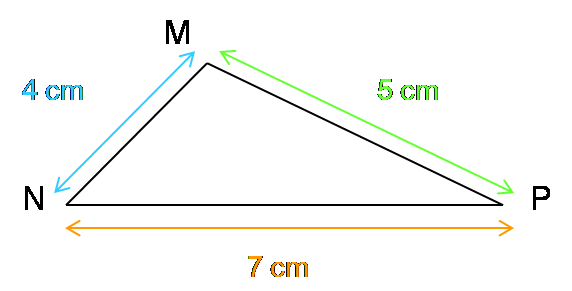
MN = 4 cm et MP + PN = 5 + 7 = 12 cm
MP = 5 cm et MN + NP = 4 + 7 = 11 cm
NP = 7 cm et NM + MP = 4 + 5 = 9 cm
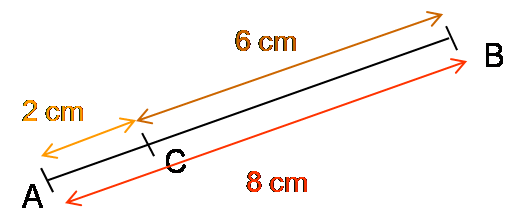On a :
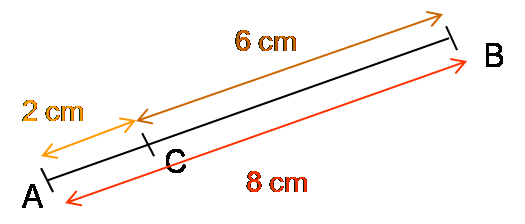
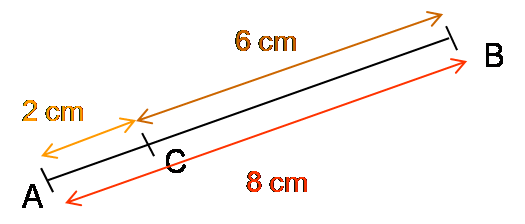
AC = 2 cm et AB + BC = 8 + 6 = 14 cm
BC = 6 cm et BA+ AC = 8 + 2 = 10 cm
AB = 8 cm et AC + CB = 2 + 6 = 8 cm
Distances parcourues : comparaison
MN = 4 cm et MP + PN = 5 + 7 = 12 cm
alors : MN
MP = 5 cm et MN + NP = 4 + 7 = 11 cm
alors : MP
NP = 7 cm et NM + MP = 4 + 5 = 9 cm
alors : NP
AC = 2 cm et AB + BC = 8 + 6 = 14 cm
alors : AC
BC = 6 cm et BA+ AC = 8 + 2 = 10 cm
alors : BC
AB = 8 cm et AC + CB = 2 + 6 = 8 cm
alors : AB = AC + CB
Distances parcourues : bilan
MN
MP
AC
Un segment étant donné, dès que l’on veut aller de l’une de ses extrémités à l’autre en passant par un point qui n’est pas sur le segment, alors le chemin est plus long.
AB = AC + CB
Un segment étant donné, si on va de l’une de ses extrémités à l’autre en passant par un point qui est sur le segment, alors la distance parcourue est la même.
Distances entre 3 points : propriétés
Soient trois points M, N et P
• Si le point P n’est pas un point du segment [MN], alors :
MN
• Si le point P est un point du segment [MN], alors :
MN = MP + PN
• Si MN = MP + PN -alors le point P est un point du segment [MN].
Inégalité triangulaire
On peut résumer les deux propriétés précédentes de la façon suivante :
Quelques soient les points M, N et P
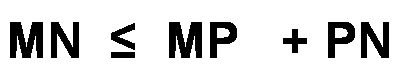
Cette relation est appelée : inégalité triangulaire.
Triangle et inégalité triangulaire
L’inégalité triangulaire permet d’affirmer que si 3 points M, N et P ne sont pas alignés :
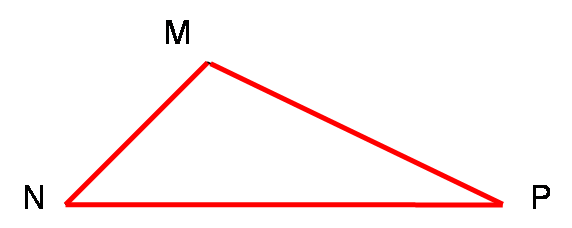MN
MP
PN
MNP est alors un triangle.
Dans ce triangle, la longueur de chacun des côtés est inférieure à la somme des longueurs des deux autres côtés.
3 longueurs et triangle
Dans un triangle, la longueur de chacun des côtés est inférieure à la somme des longueurs des deux autres côtés.
En particulier, la longueur du plus grand des 3 côtés est inférieure à la somme des deux autres.
Ici, PN
3 longueurs étant données, si la plus grande des 3 est inférieure à la somme des deux autres, alors elles sont les longueurs des 3 côtés d’un triangle.
Voici 3 segments :
Je reporte ces 3 segments de la façon suivante :
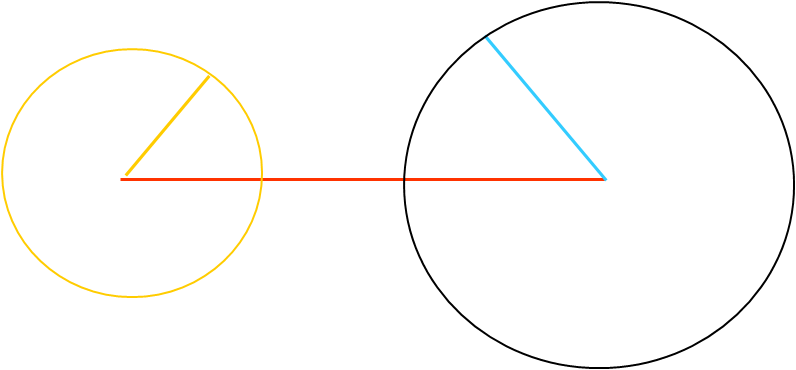On trace deux cercles ayant pour rayons les deux plus petites longueurs.
Les deux cercles ne se coupent pas, le triangle n’est pas constructible.
3 longueurs étant données, si la plus grande des 3 est supérieure à la somme des deux autres, alors on ne peut pas construire un triangle ayant ces trois longueurs pour longueurs de ses côtés.