Cours de maths à partir de 9.90 €/heure
Cours maths 3ème
Formules trigonométriques et calcul de longueurs
Ce cours a pour objectifs de démontrer dans un premier temps les formules de trigonométrie puis de les utiliser dans le but de calculer des longueurs et de travailler l’utilisation de la calculatrice. La première partie est commune avec le chapitre "Formules trigonométriques et calcul d'angles" mais l'exemple d'application en fin de chapitre diffère et s'intéresse ici au calcul de longueurs.
Formule trigonométrique : cosinus
En 4ème, on a découvert un nouvel outil appelé «
cosinus ».
Cet outil s’utilise uniquement dans les
triangles rectangles.
Le cosinus d’un angle aigu est égal au rapport :
Ce rapport ne dépend que de
la mesure de l’angle considéré.
La valeur du cosinus d’un angle est toujours comprise entre
0 et
1.
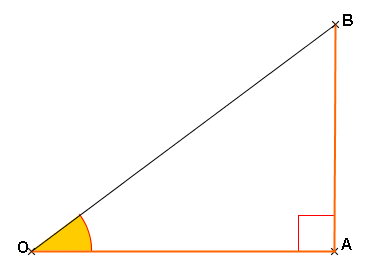
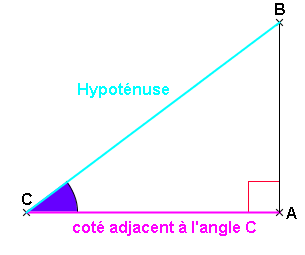
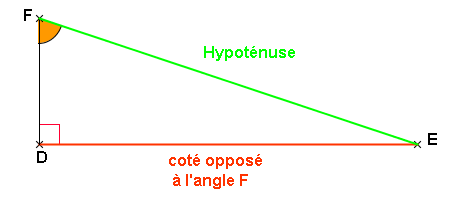
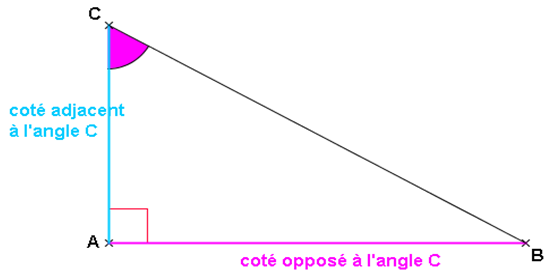
Avant de commencer …
Dans chaque cas, l’hypoténuse du triangle rectangle est surligné en couleur.


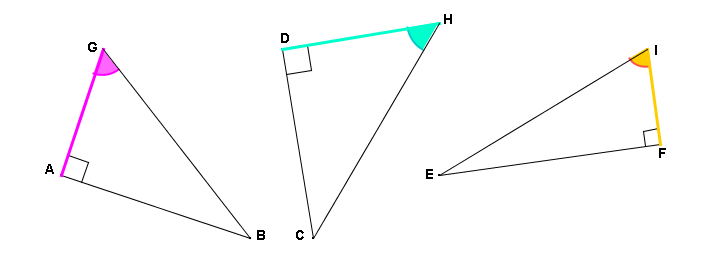
Dans chaque cas, le côté adjacent de l’angle indiqué est surligné en couleur.
J’utilise ma calculatrice ….
Avant d’utiliser la calculatrice, il faut vérifier qu’elle est bien en
mode degrés.
Voici un exemple de tableau montrant quelques valeurs de cosinus.
Les mesures d’angles sont arrondis à 1° près et les valeurs de cosinus sont arrondis à 0,01 près :
Activité : préliminaires
OAB est un triangle rectangle en A .
On place un point C sur le segment [OA], puis on trace la perpendiculaire à (OA) passant par C, elle coupe [OB] en D.
1) Faire une figure à main levée.
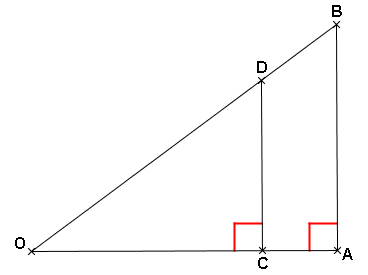
2) Que peut-on dire des droites (AB) et (CD) ? Justifier.
On sait que :
• les droites (AB) et (CD) sont perpendiculaires à une même droite (OA)
Or :
si deux droites sont perpendiculaires à une même droite alors elles sont parallèles entre elles
Donc :
(AB) // (CD)
Activité : un nouveau rapport
3) Montrer que :
En déduire que :

On sait que :
• les points O, C, A sont alignés ainsi que les points O, D, B
• (AB) // (CD)
Or :
d’après la propriété de Thalès, on a :
On a donc :
On utilise enfin le « produit en croix » :
Puis on divise les deux membres par OD ×OB :
En simplifiant, on obtient donc :
Formule trigonométrique : sinus
La valeur commune
des rapports et
ne dépend que de
la mesure de l’angle
Activité : un troisième rapport
3) Montrer que :
En déduire que :

On sait que :
• les points O, C, A sont alignés ainsi que les points O, D, B
• (AB) // (CD)
Or :
d’après la propriété de Thalès, on a :
On a donc :
On utilise enfin le « produit en croix » :
Puis on divise les deux membres par OD ×OB :
En simplifiant, on obtient donc :
Formule trigonométrique : tangente
La valeur commune des rapports et
ne dépend que de
la
la mesure de l’angle
Formule trigonométrique : cosinus d'un angle aigu
Dans un triangle rectangle, le cosinus d’un angle aigu est égal au rapport :
Ce rapport ne dépend que de la mesure de l’angle considéré.
Exemple :
Formule trigonométrique : sinus d’un angle aigu
Dans un triangle rectangle, le sinus d’un angle aigu est égal au rapport :
Ce rapport ne dépend que de la mesure de l’angle considéré.
Exemple :
En résumé
Pour utiliser les formules de trigonométrie, il faut se situer dans
un triangle rectangle.
Ces trois rapports ne dépendent que de
la mesure de l’angle considéré.
Le cosinus et le sinus d’un angle aigu sont toujours compris
entre 0 et 1.
A quoi servent ces formules ?
Ces formules permettent de calculer des longueurs de côtés et des mesures d’angles dans des triangles rectangles.
Pour retenir les 3 rapports, on peut utiliser « la formule » :
Cos
Adjacent
Hypoténuse
Sin
Opposé
Hypoténuse
Tan
Opposé
Adjacent
Exemple d’application du calcul d'angles
Exemple :
ABC est un triangle rectangle en A, tel que : AB = 6 cm et AC = 4 cm.
Calculer l’arrondi au degré de l’angle .
Méthode :
♦ On trace une figure à main levée.
On repasse en couleur les données connues et celle cherchée.
♦ Par rapport à l’angle connu, on connait le côté adjacent et on cherche la longueur du côté opposé.
On va utiliser la formule
de la tangente.
Dans le triangle ABC rectangle en B, on a :
Soit :
D'où :
Sur la calculatrice, on lit : 56,30993247
Finalement :
Propriétés des formules trigonométriques
Dans un triangle rectangle, quelle que soit la mesure x d’un angle aigu, on a :
Preuve :
2) On note :
CA le côté adjacent à l’angle x ;
CO le côté opposé à l’angle x ;
H l’hypoténuse du triangle rectangle ;
On a :
Or : dans un triangle rectangle, d’après la propriété de Pythagore, CA² + CO² = H².
Donc : cos² x + sin² x = 1
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.