Cours maths 1ère S

Fonctions trigonométriques

Fonctions trigonométriques

 

Lignes trigonométriques

• Quelques points importants à retenir :

Soit un repère orthonormé du plan et soit C le cercle trigonométrique de centre O.

Soit M un point du cercle trigonométrique et soit x un nombre réel tel que x soit une mesure en radians de l’angle .

Définitions :

Dans le repère , l'abscisse du point M est appelée le consinus de x. On le note cos x.

L'ordonnée du point M est appelée le sinus de x. On le note sin x.

La tangente de x, pour est le rapport . On la note tan x.

Propriété:

Pour tout nombre réel x, on a

et

 

Propriété fondamentale

Soit C le projeté orthogonal de M sur la droite (OI) et soit S le projeté orthogonal de M sur la droite (OJ).

Propriété :

En se plaçant dans le triangle OMC et en utilisant le théorème de Pythagore on obtient :

On en déduit, pour tout

avec

 

Valeurs remarquables

 

Etude de la fonction cosinus

Notons f(x) = cos x.

• La fonction f est définie sur .
• On a, pour tout ,

La fonction f est donc périodique de période

On peut donc restraindre l'étude de f à l'intervalle .

On a, pour tout et

La fonction f est donc paire et sa courbe représentative dans un repère orthogonal est symétrique par rapport à l'axe des ordonnées.

On peut donc restreindre l'étude de f à l'intervalle .

L'observation du cervle trogonométrique nous permet de dresser le tableau de variation de la fonction f :

Dérivabilité :

La fonction f est dérivable sur et on a, pour tout ,

f'(x) = -sin x

Démonstration

Limite :

On a

Démonstration

Courbe représentative de la fonction cosinus

 

Etude de la fonction sinus

Notons g(x) = sin x.

• La fonction g est définie sur .
• On a, pour tout ,

La fonction g est donc périodique de période .

On peut donc restreindre l'étude de g à l'intervalle .

On a, pour tout   x ∈ ℝ   − x ∈ ℝ   et

La fonction g est donc impaire et sa courbe représentative dans un repère orthogonal est symétrique par rapport à l'origine du repère.

On peut donc restreindre l'étude de g à l'intervalle .

L'observation du cercle trigonométrique nous permet de dresser le tableau de variation de la fonction g :

Dérivabilité :

La fonction g est dérivable sur ℝ et on a, pour tout x ∈ ℝ ,

g'(x) = cos x

Remarque :

Limite :

On a

Démonstration

Courbe représentative de la fonction sinus

Remarque

Les deux courbes représentatives des fonctions cosinus et sinus sont décalées de car

 

Interprétation géométrique de la tangente

Démonstration

Soit C le projeté orthogonal de M sur la droite (OI) et soit T l'intersection de (OM) et de la tangente en I au cercle.

Alors, d'après le théorème de Thalès, comme les deux droites (MC) et (TI) sont parallèles, on a

C'est à dire

d'où

Etude de la fonction tangente

Périodicité :

Propriété : La fonction tangente est périodique de période pi.

Démonstration :

On peut donc restreindre l'étude de h à l'intervalle

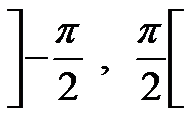
Courbe représentative de la fonction tangente

On en déduit la courbe représentative de fonction h :