Cours de maths à partir de 9.90 €/heure
4ème - Sommaire général
1. Géométrie
- Triangle rectangle
- Théorème des milieux
- Théorème de Thalès
- Théorème de Pythagore
- Triangle rectangle et cercle circonscrit
- Cosinus d'un angle aigu
- Distance d'un point à une droite
- Reconnaître une pyramide ou un cône
- Volume d'une pyramide ou d'un cône
- La démonstration en géométrie
2. Grandeurs et mesures
3. Nombres et calculs
- Multiplication de nombres relatifs
- Division de nombres relatifs
- Fractions
- Fractions - multiplication
- Fractions - division
- Addition et soustraction de fractions
- Résolution d'équations
- Résolution de problèmes à l'aide d'équations
- Comparaison de nombres relatifs
- Puissances de dix
- Calculs avec les puissances de dix
- Ecriture scientifique d'un nombre
- Puissances entières d'un nombre relatif
4. Organisation et gestion de données
- Réduction d'une expression littérale
- Développement d'une expression littérale
- Proportionnalité - produit en croix
- Pourcentages
- Proportionnalité - tableaux et graphiques
- Statistiques - introduction
- Statistiques - moyenne simple et moyenne pondérée
Cours maths - Sommaire détaillé
Géométrie
Qu'est-ce qu'un triangle est rectangle?
Ce module a pour objectif d’utiliser le théorème de Pythagore ou sa réciproque pour démontrer qu’un triangle est rectangle ou non. Il permet d’entraîner l’élève à la rédaction d’une démonstration. Ce module requiert une bonne capacité de réflexion et de calcul.
Triangles, milieux et parallèles (théorème des milieux)
Ce module a pour objectif d’expliquer le théorème des milieux et sa réciproque et d’utiliser ces deux théorèmes dans des raisonnements en géométrie. Il permet ainsi d’initier l’élève à la démonstration. Ce module peut donc constituer un bon départ pour l’année de 4ème .
Le théorème de thalès (appliqué au triangle)
Ce module a pour objectif d’utiliser le théorème de Thalès. Les exercices sont progressifs dans la difficulté. Ils permettent aussi d’initier l’élève à la démonstration et de bien comprendre le codage d’une figure. Pour ce module, l’élève doit maîtriser les calculs avec des nombres en écriture fractionnaire ainsi que l’utilisation du « produit en croix ».
Théorème de pythagore
Ce module a pour objectif d’utiliser le théorème de Pythagore. Les exercices sont progressifs dans la difficulté. Ils permettent d’initier l’élève à l’utilisation de la calculatrice au niveau des racines carrées d’un nombre positif, d’initier l’élève à la démonstration et de bien comprendre le codage d’une figure.
Triangles rectangles et cercle circonscrit
Ce module a pour objectif d’étudier les propriétés du cercle circonscrit d’un triangle rectangle et de sa médiane relative à l’hypoténuse, ainsi que les réciproques de ces propriétés. Pour aborder ce chapitre, l’élève devra mobiliser toutes ses connaissances sur la médiatrice d’un segment et les propriétés s’y rattachant.
Cosinus d'un angle aigu dans un triangle rectangle
L’objectif est d’être capable d’utiliser la relation entre le cosinus d’un angle aigu et les longueurs des deux côtés adjacents. L’élève devra aussi utiliser la calculatrice pour déterminer une valeur (exacte ou approchée) en employant les touches cos et cos-1 .
Distance d'un point par rapport à une droite
Il s’agit dans ce module d’aborder la notion de distance d’un point par rapport à une droite, celle de bissectrice d’un angle et celle de tangente d’un cercle en un point. Dans ce module, l’élève devra donc « jongler » avec plusieurs définitions et propriétés nouvelles. Il sera donc important pour l’élève de faire preuve de rigueur dans ses observations puis dans ses raisonnements.
Reconnaître une pyramide et un cône de révolution
Ce module permet à l’élève de visualiser des pyramides et des cônes de révolution par l’intermédiaire de dessins en perspective cavalière et de patrons. L’objectif est d’apprendre à l’élève à « voir dans l’espace ». Les activités, variées et simples, permettent ainsi de consolider les images mentales de l’élève relatives à des situations d’orthogonalité et de parallélisme. Ainsi, certaines activités proposées pourront faire appel à l’utilisation du théorème de Pythagore ou de sa réciproque.
Calculer le volume d'une pyramide ou d'un cône de révolution
L’objectif est d’approfondir les connaissances abordées dans le module 28 et d’utiliser une nouvelle formule ![]() en liaison avec la pratique du calcul littéral, conformément aux directives des programmes officiels. La recherche de l’aire d’une surface sera l’occasion de revenir sur les formules abordées dans les classes antérieures.
en liaison avec la pratique du calcul littéral, conformément aux directives des programmes officiels. La recherche de l’aire d’une surface sera l’occasion de revenir sur les formules abordées dans les classes antérieures.
Initiation à la démonstration en géométrie
La démonstration est une notion importante au collège et notamment en 4ème. Le premier objectif est de faire comprendre à l’élève le sens des théorèmes qu’il utilise et de faciliter leur utilisation. Le deuxième est d’amener l’élève à une compréhension des critères d’une démonstration valide afin qu’il prenne en charge la vérification et l’écriture rigoureuse de celle-ci. Chaque enseignant a la charge d’améliorer les conceptions des élèves concernant la démonstration. Et, en général, elles sont multiples (!). La communication entre les élèves et l’enseignant sera donc prépondérante pour palier aux différents problèmes de rédaction des démonstrations. Ce module propose donc de reprendre les résultats vus en 5ème pour les réinvestir dans des raisonnements en géométrie. Par ce biais-là, l’utilisation du vocabulaire propre à la rédaction d’une petite démonstration (si, alors, donc, or, car, comme, …) devrait se mettre en place et permettre à l’élève de faire évoluer ses conceptions sur le raisonnement mathématique en géométrie et de comprendre ce qui est attendu de lui en 4ème.
Grandeurs et mesures
Agrandissement et réduction
Ce module vise à étudier les propriétés d’un agrandissement ou d’une réduction : conservation des angles, du parallélisme, multiplication des longueurs par un coefficient, … Certaines situations pourront être analysées grâce à l’utilisation du théorème de Thalès.
La démonstration à la fin de la 4ème
Ce module est destiné à faire le point pour l’élève sur ses conceptions au niveau de la démonstration. On reprend alors, dans ce module, tous les théorèmes, les propriétés et les définitions abordés en 4ème dans des exercices où il faudra rédiger des démonstrations.
Grandeurs - Quotients
Il s’agit d’utiliser la formule V = d/t dans des situations diverses, ce module est donc en liaison avec la pratique du calcul littéral. Il permet d’exploiter des situations riches où le raisonnement mathématique peut être très intéressant. C’est aussi l’occasion pour l’élève de se familiariser avec le vocabulaire kilomètre-heure et les notations : km/h, m/s, ou encore km.h-1, m.s-1, …
Nombres et calcul
Multiplication des nombres relatifs
Ce module a pour objectif d’effectuer des multiplications avec les nombres relatifs. Les exercices sont progressifs dans la difficulté. Le travail est axé sur la détermination du signe et de la distance à zéro d’un produit de deux ou plusieurs facteurs. Cette notion pourra être reliée aux modules sur les puissances entières d’un nombre relatif.
Division des nombres relatifs
Ce module a pour objectif d’effectuer des divisions avec les nombres relatifs. Les exercices sont progressifs dans la difficulté. Le travail est axé sur la détermination du signe et de la distance à zéro d’un quotient. Cette notion pourra être reliée aux modules sur les puissances entières d’un nombre relatif.
Ecriture fractionnaire 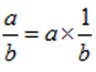
Ce module a pour objectif de revenir sur les notions de quotient et de partage afin d’homogénéiser les connaissances vues en 6ème et 5ème et de partir d’un bon pied en 4ème. Les exercices permettent de reprendre certaines règles de calculs avec les nombres en écriture fractionnaire. Ils constituent aussi un bon entraînement au calcul mental. Des problèmes concrets sont proposés et sont conçus pour activer une réflexion autour du calcul.
Multiplication des nombres en écriture fractionnaire
Ce module a pour objectif d’effectuer des multiplications avec les nombres en écriture fractionnaire. Il permet d’aborder aussi la simplification des fractions dans des situations de calculs. Des situations concrètes sont proposées et sont conçues pour activer une réflexion autour du calcul et pour donner du sens à ce type d’opération.
Division des nombres en écriture fractionnaire
Ce module a pour objectif d’effectuer des divisions avec les nombres en écriture fractionnaire. Il permet d’effectuer des calculs simples, ils sont progressifs dans la difficulté. Des situations concrètes sont proposées afin de permettre à l’élève de donner du sens aux calculs qu’il effectue.
Addition et soustraction des nombres en écriture fractionnaire
Ce module a pour objectif d’effectuer des additions et des soustractions avec les nombres en écriture fractionnaire. Il permet d’effectuer des calculs simples, ils sont progressifs dans la difficulté. Des situations concrètes sont proposées afin de permettre à l’élève de donner du sens aux calculs qu’il effectue.
Résoudre des équations
Ce module a pour objectif d’entraîner l’élève à résoudre de façon rigoureuse les équations qu’il pourra rencontrer en classe de 4ème . Il est cependant utile de rappeler que ce module traite en priorité de la partie « technique » de la résolution des équations mais que cet apprentissage ne peut être dissocié de la résolution de problèmes concrets (partie du programme de 4ème traitée dans le module 10), ce qui donne tout son sens aux équations et à leur résolution. L’élève doit en avoir conscience pour ne pas se limiter à la partie « mécanique » des calculs qu’engendre la résolution des équations.
Résoudre des problèmes à l'aide d'équations
Ce module a pour but de traiter la résolution de problèmes à l’aide d’équations, conformément au programme officiel de la classe de 4ème . L’accent est alors mis sur l’enchaînement des étapes de résolution de tels problèmes, c’est-à-dire : mise en équation, résolution de l’équation et interprétation du résultat. Ce module demande à l’élève de bien maîtriser la résolution des équations.
Comparer des nombres relatifs
Dans un premier temps nous revenons sur les inégalités strictes (avec l’utilisation des symboles ![]() ) abordées les années précédentes. Dans un deuxième temps nous approfondissons le sujet avec l’utilisation des inégalités au sens large (avec l’utilisation des symboles ) et nous abordons les effets des opérations sur l’ordre dans l’objectif de se préparer à la résolution des inéquations qui est une notion abordée en 3ème.
) abordées les années précédentes. Dans un deuxième temps nous approfondissons le sujet avec l’utilisation des inégalités au sens large (avec l’utilisation des symboles ) et nous abordons les effets des opérations sur l’ordre dans l’objectif de se préparer à la résolution des inéquations qui est une notion abordée en 3ème.
Puissances de dix (définition)
Ce module est destiné à introduire la notion des puissances de dix. L’usage des puissances de dix dans les matières scientifiques, notamment en Physique et en SVT où on aborde le domaine microscopique et les échelles astronomiques, doit faire partie d’un apprentissage régulier et progressif.
Calculs avec les puissances de dix
Ce module a pour objectif d’utiliser sur des exemples numériques les égalités :
![]() où m et n sont des entiers relatifs.
où m et n sont des entiers relatifs.
Les exercices portent notamment sur des situations concrètes (par ex : les unités de mesures utilisées dans les sciences expérimentales).
L'écriture scientifique d'un nombre
L’objectif est de permettre à l’élève d’écrire un nombre décimal sous différentes formes faisant intervenir des puissances de dix et de reconnaître l’écriture scientifique d’un nombre. Ce module nécessite que l’élève maîtrise un minimum les calculs avec les puissances de dix.
Puissances entières d'un nombre relatif
Il s’agit, dans ce module, de comprendre les notations ![]() et de savoir utiliser ces notations dans des calculs. Certaines égalités du type
et de savoir utiliser ces notations dans des calculs. Certaines égalités du type ![]() , … seront abordées mais il est bien spécifié dans les programmes officiels que les exposants seront des nombres entiers très simples et ne doivent pas donner lieu à des calculs superficiels. Le principal objectif de ce module est donc de permettre de donner du sens à ces notations et de s’appuyer sur leurs significations pour résoudre des calculs simples.
, … seront abordées mais il est bien spécifié dans les programmes officiels que les exposants seront des nombres entiers très simples et ne doivent pas donner lieu à des calculs superficiels. Le principal objectif de ce module est donc de permettre de donner du sens à ces notations et de s’appuyer sur leurs significations pour résoudre des calculs simples.
Organisation et gestion de données
Calculer des valeurs et réduire des expressions littérales
Ce module a pour objectif d’expliquer ce qu’est une expression littérale et d’utiliser les expressions littérales dans des calculs numériques. Le but est aussi de pouvoir « jongler » avec les différentes écritures d’une même expression littérale, ce qui pourra faciliter la résolution de problèmes plus complexes par la suite.
Développer des expressions littérales
Ce module a pour objectif d’apprendre à développer des expressions littérales de la forme k(a+b) ou encore (a+b)(c+d). A noter que le cours utilise une approche géométrique classique pour permettre à l’élève de donner du sens au développement des expressions littérales et que les activités de développement proposées dans ce module visent à prolonger celles qui ont été pratiquées au niveau Cinquième. Il est important que l’élève sache réduire des expressions car c’est une notion que l’on rencontrera souvent dans les exercices de ce module.
Déterminer une quatrième proportionnelle
Le programme de 4ème expose la volonté de poursuivre l’étude de la proportionnalité introduite dans les classes antérieures. Aux divers moyens utilisés en 6ème et en 5ème pour déterminer une quatrième proportionnelle s’ajoute une nouvelle méthode connue sous le nom de « produit en croix » qui est justifiée par l’égalité 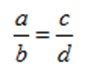 et qui est liée avec de nombreuses parties du programme de 4ème (Notamment : l’utilisation des fractions, l’utilisation des égalités, la résolution d’équations, …). Ce module a donc pour objectif d’exposer cette nouvelle méthode et de permettre à l’élève de la pratiquer dans des situations concrètes afin de lui donner un sens.
et qui est liée avec de nombreuses parties du programme de 4ème (Notamment : l’utilisation des fractions, l’utilisation des égalités, la résolution d’équations, …). Ce module a donc pour objectif d’exposer cette nouvelle méthode et de permettre à l’élève de la pratiquer dans des situations concrètes afin de lui donner un sens.
Déterminer un pourcentage relatif à un caractère
Certaines situations de la vie courante font appel à l’utilisation des pourcentages. Ce module vise à plonger directement l’élève dans ces situations pour lui permettre de mieux comprendre le sens des calculs qu’il effectue. Un des principaux outils utilisés est le « produit en croix ». Il est donc important que l’élève sache l’utiliser pour profiter de ce module.
Situations de proportionnalité (graphiques et tableaux)
Ce module a pour objectif de faire travailler l’élève sur des situations de proportionnalité et de non proportionnalité en utilisant la caractérisation de la proportionnalité par l’alignement des points avec l’origine dans un repère.
Séries de données statistiques
Ce module aborde la notion de série statistique. L’objectif est de familiariser l’élève avec le vocabulaire (effectif, fréquence, effectif cumulé, fréquence cumulée, …). Il traite de notions que l’on peut rencontrer dans d’autres matières en 4ème : Technologie, Histoire-Géographie, les sciences expérimentales, …etc. A noter que c’est aussi le prétexte pour faire des lectures et des interprétations de tableaux et de graphiques.
Moyenne et moyenne pondérée d'une série statistique
Le premier objectif est de permettre à l’élève de calculer des moyennes trimestrielles, les siennes par exemple, et des moyennes utiles pour d’autres situations tout aussi importantes… Le deuxième objectif est d’apprendre à l’élève à interpréter des moyennes et de comprendre les différences entre ces moyennes.
Sommaires
Vous avez choisi le créneau suivant :
Nous sommes désolés, mais la plage horaire choisie n'est plus disponible.
Nous vous invitons à choisir un autre créneau.